【题目】列方程解应用题:某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)

(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙种商品是按原价打几折销售?
参考答案:
【答案】(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获利1950元;(2)第二次乙种商品是按原价打![]() 折销售
折销售
【解析】
(1)设第一次购进甲商品x件,则购进乙商品(![]() x+15)件,根据题意列出方程即可求出x的值,然后根据“获利=售价-进价”即可求出结论;
x+15)件,根据题意列出方程即可求出x的值,然后根据“获利=售价-进价”即可求出结论;
(2)设第二次乙种商品是按原价打y折销售,根据题意列出方程即可求出结论.
解:(1)设第一次购进甲商品x件,则购进乙商品(![]() x+15)件
x+15)件
由题意可得:22x+30(![]() x+15)=6000
x+15)=6000
解得:x=150
∴购进乙商品![]() ×150+15=90件
×150+15=90件
∴全部卖完后一共可获利(29-22)×150+(40-30)×90=1950(元)
答:该超市将第一次购进的甲、乙两种商品全部卖完后一共可获利1950元.
(2)设第二次乙种商品是按原价打y折销售
由题意可得:(29-22)×150+(40×![]() -30)×90×3-1950=180
-30)×90×3-1950=180
解得:y=![]()
答:第二次乙种商品是按原价打![]() 折销售.
折销售.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)尺规作图:如图1,请在x轴上作出表示(
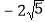 ,0)的点(保留清晰作图痕迹,不写作法).
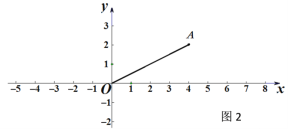
,0)的点(保留清晰作图痕迹,不写作法).(2)如图2,已知点A(4,2),点B在x轴上,若∠OAB=90°,试求点B的坐标;
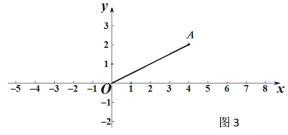
(3)如图3,已知点A(4,2),点C在x轴上,若△OAC为等腰三角形,试求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.
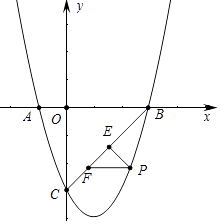
(1)求抛物线的解析式;
(2)如图所示,直线BC下方的抛物线上有一点P,过点p作PE⊥BC于点E,作PF平行于x轴交直线BC于点F,求△PEF周长的最大值;
(3)已知点M是抛物线的顶点,点N是y轴上一点,点Q是坐标平面内一点,若点P是抛物线上一点,且位于抛物线的对称轴右侧,是否存在以P、M、N、Q为顶点且以PM为边的正方形?若存在,直接写出点P的横坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和直线BC相交于点B,连接AC,点D. E. H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°,
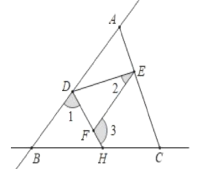
(1)求证:∠CEF=∠EAD;
(2)若DH平分∠BDE,∠2=α,求∠3的度数.(用α表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a∥b,直线l与a、b分别相交于A,B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )
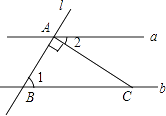
A.58°
B.42°
C.32°
D.28° -
科目: 来源: 题型:
查看答案和解析>>【题目】实数a,b在数轴上对应点的位置如图所示,化简|a|+
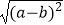 的结果是( )
的结果是( )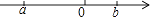
A.﹣2a+b
B.2a﹣b
C.﹣b
D.b -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为t.

(1)当t=1时,PD=2AC,请求出AP的长;
(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
相关试题

