【题目】某校开设武术、舞蹈、剪纸三项活动课程,为了了解学生对这三项活动课程的兴趣情况,随机抽取了部分学生进行调查(每人从中只能选一顶),并将调查结果绘制成下面两幅统计图,请你结合图中信息解答问题.

(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是___;
(3)在扇形统计图中,计算女生喜欢剪纸活动课程人数对应的圆心角度数;
(4)已知该校有1200名学生,请结合数据简要分析该校学生对剪纸课程的兴趣情况.
参考答案:
【答案】(1)见解析;(2)100;(3)115.2°;(4)全校喜欢剪纸的学生360人
【解析】
(1)根据扇形统计图可得出女生喜欢武术的占20%,利用条形图中喜欢武术的女生有10人,即可求出女生总人数,即可得出喜欢舞蹈的人数;
(2)根据(1)的计算结果再利用条形图即可得出样本容量;
(3)360°乘以女生中剪纸类人数所占百分比即可得;
(4)用全校学生数×喜欢剪纸的学生在样本中所占比例即可求出.
解:(1)被调查的女生人数为10÷20%=50人,
则女生舞蹈类人数为50﹣(10+16)=24人,
补全图形如下:
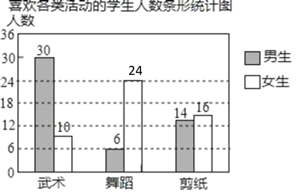
(2)样本容量为50+30+6+14=100,
故答案为100;
(3)扇形图中剪纸类所占的圆心角度数为360°×![]() =115.2°;
=115.2°;
(4)估计全校学生中喜欢剪纸的人数是1200×![]() =360,
=360,
全校喜欢剪纸的学生有360人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市决定购买A、B两种树苗对某段道路进行绿化改造,已知购买A种树苗9棵,B种树苗4棵,需要700元;购买A种树苗3棵,B种树苗5棵,则需要380元.
(1)求购买A、B两种树苗每颗各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于60棵,且用于购买这两种树苗的资金不能超过5260元.若购进这两种树苗共100棵,则有哪几种购买方案?哪种方案最省钱? -
科目: 来源: 题型:
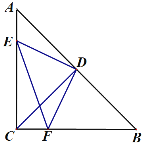
查看答案和解析>>【题目】如图在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,点E、F分别在AC、BC上,且∠EDF=90°.
(1)求证:△AED≌△CFD;
(2)试判断CE、CF与CD之间的数量关系,并说明理由;
(3)若CF=1,CE=3,试求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠ACD=90°,AC=DC,MN是过点A的直线,过点D作DB⊥MN于点B,连接CB.
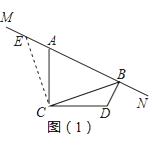
(1)问题发现
如图(1),过点C作CE⊥CB,与MN交于点E,则易发现BD和EA之间的数量关系为 , BD、AB、CB之间的数量关系为 .
(2)拓展探究
当MN绕点A旋转到如图(2)位置时,BD、AB、CB之间满足怎样的数量关系?请写出你的猜想,并给予证明.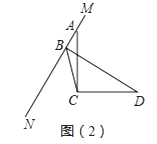
(3)解决问题
当MN绕点A旋转到如图(3)位置时(点C、D在直线MN两侧),若此时∠BCD=30°,BD=2时,CB= .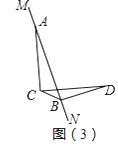
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,O为直线AB上一点,∠DOE=90°.
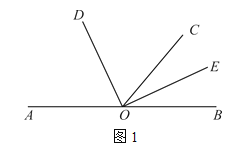
(1)如图1,若∠AOC=130°,OD平分∠AOC.
①求∠BOD的度数;
②请通过计算说明OE是否平分∠BOC.
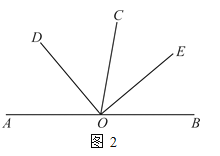
(2)如图2,若∠BOE:∠AOE=2:7,求∠AOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)尺规作图:如图1,请在x轴上作出表示(
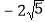 ,0)的点(保留清晰作图痕迹,不写作法).
,0)的点(保留清晰作图痕迹,不写作法).(2)如图2,已知点A(4,2),点B在x轴上,若∠OAB=90°,试求点B的坐标;
(3)如图3,已知点A(4,2),点C在x轴上,若△OAC为等腰三角形,试求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.
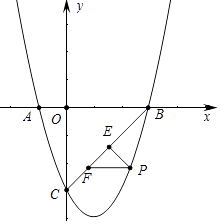
(1)求抛物线的解析式;
(2)如图所示,直线BC下方的抛物线上有一点P,过点p作PE⊥BC于点E,作PF平行于x轴交直线BC于点F,求△PEF周长的最大值;
(3)已知点M是抛物线的顶点,点N是y轴上一点,点Q是坐标平面内一点,若点P是抛物线上一点,且位于抛物线的对称轴右侧,是否存在以P、M、N、Q为顶点且以PM为边的正方形?若存在,直接写出点P的横坐标;若不存在,说明理由.
相关试题

