【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x(x大于0)秒.
(1)点C表示的数是 ;
(2)当x= 秒时,点P到达点A处?
(3)运动过程中点P表示的数是 (用含字母x的式子表示);
(4)当P,C之间的距离为2个单位长度时,求x的值.
![]()
参考答案:
【答案】(1)1(2)当x=5秒时,点P到达点A处(3)2x﹣4(4)当x等于1.5或3.5秒时,P、C之间的距离为2个单位长度
【解析】
(1)根据题意得到点C是AB的中点;
(2)、(3)根据点P的运动路程和运动速度列出方程;
(4)分两种情况:点P在点C的左边有右边.
(1)依题意得,点C是AB的中点,故点C表示的数是:![]() =1.
=1.
故答案为:1;
(2)[6﹣(﹣4)]÷2=10÷2=5(秒)
答:当x=5秒时,点P到达点A处.
(3)点P表示的数是2x﹣4.
故答案是:2x﹣4;
(4)当点P在点C的左边时,2x=3,则x=1.5;
当点P在点C的右边时,2x=7,则x=3.5.
综上所述,当x等于1.5或3.5秒时,P、C之间的距离为2个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校要举办一次演讲比赛,每班只能选一人参加比赛.但八年级一班共有甲、乙两人的演讲水平相不相上下,现要在他们两人中选一人去参加全校的演讲比赛,经班主任与全班同学协商决定用摸小球的游戏来确定谁去参赛(胜者参赛). 游戏规则如下:在两个不透明的盒子中,一个盒子里放着两个红球,一个白球;另一个盒子里放着三个白球,一个红球,从两个盒子中各摸一个球,若摸得的两个球都是红球,甲胜;摸得的两个球都是白球,乙胜,否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止.
根据上述规则回答下列问题:
(1)从两个盒子各摸出一个球,一个球为白球,一个球为红球的概率是多少?
(2)该游戏公平吗?请用列表或树状图等方法说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC为⊙O的直径,A为圆上一点,点F为
 的中点,延长AB、AC,与过F点的切线交于D、E两点.
的中点,延长AB、AC,与过F点的切线交于D、E两点. 
(1)求证:BC∥DE;
(2)若BC:DF=4:3,求tan∠ABC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知函数
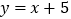 的图象与反比例函数
的图象与反比例函数 的图象的一个交点为A
的图象的一个交点为A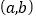 ,则
,则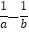 = ________.
= ________.(2)如果
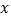 满足
满足 ,试求代数式
,试求代数式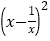 的值.
的值.(3)已知
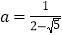 ,
,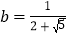 ,求
,求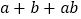 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+1过A(1,0)、B,(5,0)两点.

(1)求:抛物线的函数表达式;
(2)求:抛物线与y轴的交点C的坐标及其对称轴
(3)若抛物线对称轴上有一点P,使△COA∽△APB,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
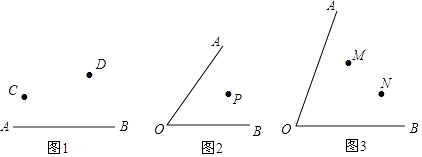
(1)如图1,在AB直线一侧C、D两点,在AB上找一点P,使C、D、P三点组成的三角形的周长最短,找出此点并说明理由.
(2)如图2,在∠AOB内部有一点P,是否在OA、OB上分别存在点E、F,使得E、F、P三点组成的三角形的周长最短,找出E、F两点,并说明理由.
(3)如图3,在∠AOB内部有两点M、N,是否在OA、OB上分别存在点E、F,使得E、F、M、N,四点组成的四边形的周长最短,找出E、F两点,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)某校有学生2000名,为了了解学生在篮球、足球、排球和乒乓球这四项球类运动中最喜爱的一项球类运动情况,对学生开展了随机调查,丙将结果绘制成如下的统计图.

请根据以上信息,完成下列问题:
(1)本次调查的样本容量是 ;
(2)某位同学被抽中的概率是 ;
(3)据此估计全校最喜爱篮球运动的学生人数约有 名;
(4)将条形统计图补充完整.
相关试题

