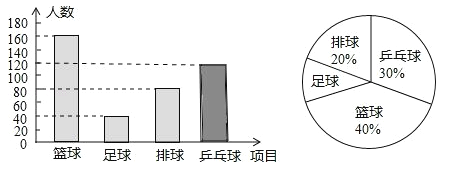
【题目】(8分)某校有学生2000名,为了了解学生在篮球、足球、排球和乒乓球这四项球类运动中最喜爱的一项球类运动情况,对学生开展了随机调查,丙将结果绘制成如下的统计图.

请根据以上信息,完成下列问题:
(1)本次调查的样本容量是 ;
(2)某位同学被抽中的概率是 ;
(3)据此估计全校最喜爱篮球运动的学生人数约有 名;
(4)将条形统计图补充完整.
参考答案:
【答案】(1)400;(2)![]() ;(3)800;(4)答案见试题解析.
;(3)800;(4)答案见试题解析.
【解析】
试题(1)用篮球的人数除以篮球的百分比,即可得到结论;
(2)根据概率公式即可得到结论;
(3)根据样本估计总体,即可得到结论;
(4)计算出乒乓球的人数,即可得到结论.
试题解析:(1)160÷40%=400(人),即本次调查的样本容量是400.故答案为:400.
(2)400÷2000=![]() .故答案为:
.故答案为:![]() .
.
(3)2000×40%=800(人).故答案为:800.
(4)乒乓球的人数:400×30%=120(人).
如图所示:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x(x大于0)秒.
(1)点C表示的数是 ;
(2)当x= 秒时,点P到达点A处?
(3)运动过程中点P表示的数是 (用含字母x的式子表示);
(4)当P,C之间的距离为2个单位长度时,求x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+1过A(1,0)、B,(5,0)两点.

(1)求:抛物线的函数表达式;
(2)求:抛物线与y轴的交点C的坐标及其对称轴
(3)若抛物线对称轴上有一点P,使△COA∽△APB,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
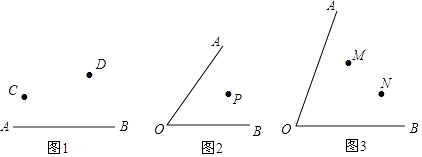
(1)如图1,在AB直线一侧C、D两点,在AB上找一点P,使C、D、P三点组成的三角形的周长最短,找出此点并说明理由.
(2)如图2,在∠AOB内部有一点P,是否在OA、OB上分别存在点E、F,使得E、F、P三点组成的三角形的周长最短,找出E、F两点,并说明理由.
(3)如图3,在∠AOB内部有两点M、N,是否在OA、OB上分别存在点E、F,使得E、F、M、N,四点组成的四边形的周长最短,找出E、F两点,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A.a0=1
B.a﹣1=﹣a
C.a3a2=a5
D.2a2+3a3=5a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①, 然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,
②﹣①得,3S﹣S=39﹣1,即2S=39﹣1,
所以S= .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 . -
科目: 来源: 题型:
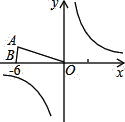
查看答案和解析>>【题目】已知:等腰△OAB在直角坐标系中的位置如图,点A坐标为
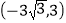 ,点B坐标为(-6,0).
,点B坐标为(-6,0).(1)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数
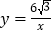 的图象上,求a的值;
的图象上,求a的值;(2)若△OAB绕点O按逆时针方向旋转α度(0<α<360).
①当α=30°时,点B恰好落在反比例函数
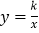 的图象上,求k的值;
的图象上,求k的值;②问点A、B能否同时落在①中的反比例函数的图象上?若能,直接写出α的值;若不能,请说明理由.
相关试题

