【题目】某学校要举办一次演讲比赛,每班只能选一人参加比赛.但八年级一班共有甲、乙两人的演讲水平相不相上下,现要在他们两人中选一人去参加全校的演讲比赛,经班主任与全班同学协商决定用摸小球的游戏来确定谁去参赛(胜者参赛). 游戏规则如下:在两个不透明的盒子中,一个盒子里放着两个红球,一个白球;另一个盒子里放着三个白球,一个红球,从两个盒子中各摸一个球,若摸得的两个球都是红球,甲胜;摸得的两个球都是白球,乙胜,否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止.
根据上述规则回答下列问题:
(1)从两个盒子各摸出一个球,一个球为白球,一个球为红球的概率是多少?
(2)该游戏公平吗?请用列表或树状图等方法说明理由.
参考答案:
【答案】
(1)解:画树状图如下:
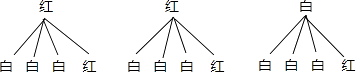
由树状图可知,共有12种等可能情形,其中一个球为白球,一个球为红球的有7种,
∴一个球为白球,一个球为红球的概率是 ![]()
(2)解:由(1)中树状图可知,P(甲获胜)= ![]() =
= ![]() ,P(乙获胜)=
,P(乙获胜)= ![]() =
= ![]() ,
,
∵ ![]()
![]() ,
,
∴该游戏规则不公平
【解析】(1)画树状图列出所有等可能结果数,再根据概率公式计算即可得;(2)分别求出甲获胜和乙获胜的概率,比较后即可得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
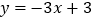 与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线
与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线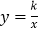 (
(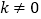 )上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线
)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线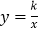 (
(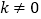 )上的点D1处,则a= .
)上的点D1处,则a= .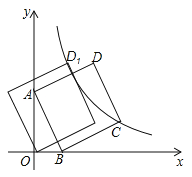
-
科目: 来源: 题型:
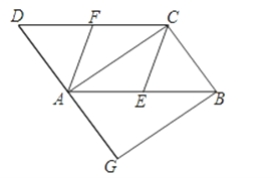
查看答案和解析>>【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
(1)求证:CE∥AF;
(2)若∠G=90°,求证:四边形CEAF是菱形.
-
科目: 来源: 题型:
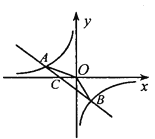
查看答案和解析>>【题目】如图,已知A(-4,n),B(2,-4)是一次函数
 的图像和反比例函数
的图像和反比例函数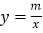 的图像的两个交点.
的图像的两个交点.(1)求反比例函数和一次函数的解析式;
(2)求不等式
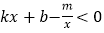 的解集_________(请直接写出答案).
的解集_________(请直接写出答案).(3)求△AOB的面积;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC为⊙O的直径,A为圆上一点,点F为
 的中点,延长AB、AC,与过F点的切线交于D、E两点.
的中点,延长AB、AC,与过F点的切线交于D、E两点. 
(1)求证:BC∥DE;
(2)若BC:DF=4:3,求tan∠ABC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知函数
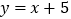 的图象与反比例函数
的图象与反比例函数 的图象的一个交点为A
的图象的一个交点为A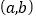 ,则
,则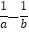 = ________.
= ________.(2)如果
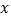 满足
满足 ,试求代数式
,试求代数式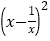 的值.
的值.(3)已知
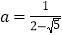 ,
,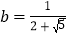 ,求
,求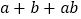 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x(x大于0)秒.
(1)点C表示的数是 ;
(2)当x= 秒时,点P到达点A处?
(3)运动过程中点P表示的数是 (用含字母x的式子表示);
(4)当P,C之间的距离为2个单位长度时,求x的值.

相关试题

