【题目】从2开始,连续的偶数相加,它们和的情况如下表:
加数的个数 | 连续偶数的和 |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
(1)如果![]() 时,那么
时,那么![]() 的值为______;
的值为______;
(2)根据表中的规律猜想:用含有![]() 的代数式表示
的代数式表示![]() 的公式为:
的公式为:![]() ______;
______;
(3)根据上题的规律计算![]() 的值(要有计算过程).
的值(要有计算过程).
参考答案:
【答案】(1)72;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据表中的规律发现:第n个式子的和是n(n+1),把n=8代入求得数值即可;(2)根据特殊的式子即可发现规律;(3)结合上述规律,只需加上2+4+…+2020再减去2+4+…+198即可计算.
(1)根据题意:第n个式子的和是n(n+1).则当n=8时,S=8×9=72;
(2)根据特殊的式子即可发现规律,S=S=2+4+6+8+…+2n=2(1+2+3+…+n)=n(n+1);
(3)![]()
![]()
![]()
![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
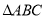 中,
中,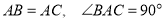 ,点
,点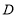 在射线
在射线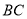 上(与
上(与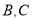 两点不重合),以
两点不重合),以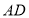 为边作正方形
为边作正方形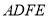 ,使点
,使点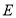 与点
与点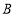 在直线
在直线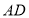 的异侧,射线
的异侧,射线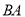 与直线
与直线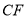 相交于点
相交于点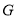 .
.(1)若点
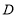 在线段
在线段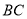 上,如图(1),判断:线段
上,如图(1),判断:线段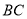 与线段
与线段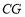 的数量关系: ,位置关系: .
的数量关系: ,位置关系: .(2)如图(2),①若点
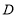 在线段
在线段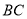 的延长线上,(1)中判断线段
的延长线上,(1)中判断线段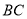 与线段
与线段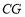 的数量关系与位置关系是否仍然成立,并说明理由;
的数量关系与位置关系是否仍然成立,并说明理由;②当
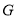 为
为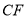 中点,
中点,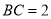 时,求线段
时,求线段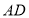 的长.
的长.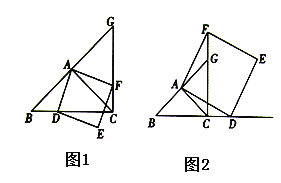
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机王师傅从上午8:10~9:25在合肥市巢湖大堤环岛路上一段东西方向路段上营运,共连续运载十批乘客.若规定向东为正,向西为负,王师傅运载十批乘客的里程如下:(单位:千米)+9,-7,+3,-8,+8,+5,-9,-4,+4,+3
(1)将最后一批乘客送到目的地时,王师傅距离第一批乘客出发地的位置怎样?距离多少千米?
(2)上午8:10~9:25王师傅开车的平均速度是多少?
(3)若出租车的收费标准为:起步价8元(不超过3千米),超过3千米,超过部分每千米1.5元.则王师傅在上午8:10~9:25一共收入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上点A,B,C的位置如图,点C是线段AB的中点,点A表示的数比点C表示的数的两倍还大3,点B和点C表示的数是互为相反数,点C表示的数是__________.
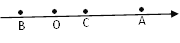
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
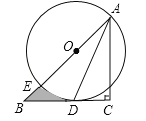
相关试题

