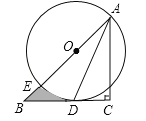
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接DE,OD.利用弦切角定理,直径所对的圆周角是直角,等角的余角相等证明∠DAO=∠CAD,进而得出结论;
(2)根据等腰三角形的性质得到∠B=∠BAC=45°,由BC相切⊙O于点D,得到∠ODB=90°,求得OD=BD,∠BOD=45°,设BD=x,则OD=OA=x,OB=![]() x,根据勾股定理得到BD=OD=
x,根据勾股定理得到BD=OD=![]() ,于是得到结论.
,于是得到结论.
试题解析:解:(1)证明:连接DE,OD.
∵BC相切⊙O于点D,∴∠CDA=∠AED,∵AE为直径,∴∠ADE=90°,∵AC⊥BC,∴∠ACD=90°,∴∠DAO=∠CAD,∴AD平分∠BAC;
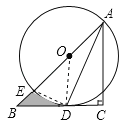
(2)∵在Rt△ABC中,∠C=90°,AC=BC,∴∠B=∠BAC=45°,∵BC相切⊙O于点D,∴∠ODB=90°,∴OD=BD,∴∠BOD=45°,设BD=x,则OD=OA=x,OB=![]() x,∴BC=AC=x+1,∵AC2+BC2=AB2,∴2(x+1)2=(
x,∴BC=AC=x+1,∵AC2+BC2=AB2,∴2(x+1)2=(![]() x+x)2,∴x=
x+x)2,∴x=![]() ,∴BD=OD=
,∴BD=OD=![]() ,∴图中阴影部分的面积=S△BOD﹣S扇形DOE=
,∴图中阴影部分的面积=S△BOD﹣S扇形DOE=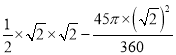 =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2开始,连续的偶数相加,它们和的情况如下表:
加数的个数
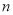
连续偶数的和
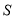
1
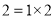
2
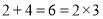
3
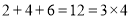
4
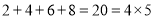
5
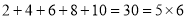
(1)如果
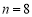 时,那么
时,那么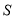 的值为______;
的值为______;(2)根据表中的规律猜想:用含有
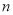 的代数式表示
的代数式表示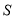 的公式为:
的公式为: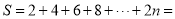 ______;
______;(3)根据上题的规律计算
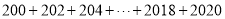 的值(要有计算过程).
的值(要有计算过程). -
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机王师傅从上午8:10~9:25在合肥市巢湖大堤环岛路上一段东西方向路段上营运,共连续运载十批乘客.若规定向东为正,向西为负,王师傅运载十批乘客的里程如下:(单位:千米)+9,-7,+3,-8,+8,+5,-9,-4,+4,+3
(1)将最后一批乘客送到目的地时,王师傅距离第一批乘客出发地的位置怎样?距离多少千米?
(2)上午8:10~9:25王师傅开车的平均速度是多少?
(3)若出租车的收费标准为:起步价8元(不超过3千米),超过3千米,超过部分每千米1.5元.则王师傅在上午8:10~9:25一共收入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上点A,B,C的位置如图,点C是线段AB的中点,点A表示的数比点C表示的数的两倍还大3,点B和点C表示的数是互为相反数,点C表示的数是__________.
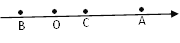
-
科目: 来源: 题型:
查看答案和解析>>【题目】首条贯通丝绸之路经济带的高铁线﹣宝兰客专进入全线拉通试验阶段,宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行一下探究:
【信息读取】
(1)西宁到西安两地相距 千米,两车出发后 小时相遇;
(2)普通列车到达终点共需 小时,普通列车的速度是 千米/小时.
【解决问题】
(3)求动车的速度;
(4)普通列车行驶t小时后,动车到达终点西宁,求此时普通列车还需行驶多少千米到达西安?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c+1。
(1)当b=1时,求这个二次函数的对称轴的方程;
(2)若c=﹣
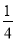 b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?(3)若二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,b>0,与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足
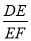 =
=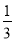 ,求二次函数的表达式.
,求二次函数的表达式.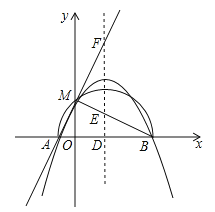
-
科目: 来源: 题型:
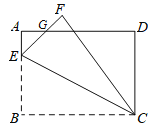
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=6,E为AB上一点,将△BCE沿CE翻折至△FCE,EF与AD相交于点G,且AG=FG,则线段AE的长为__________.
相关试题

