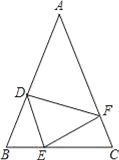
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
(4)请你猜想:当∠A为多少度时,∠EDF+∠EFD=120°,并请说明理由.
参考答案:
【答案】(1)证明见解析;(2)∠DEF=70°; (3)△DEF不可能是等腰直角三角形,理由见解析;(4)当∠A=60°时,∠EDF+∠EFD=120°,理由见解析.
【解析】
(1)首先根据条件证明△DBE≌△ECF,根据全等三角形的性质可得DE=FE,进而可得到△DEF是等腰三角形;
(2)由(1)中的全等得出∠BDE=∠CEF,再由角之间的转化,从而可求解∠DEF的大小;(3)由于AB=AC,可得∠B=∠C≠90°=∠DEF,从而可确定其不可能是等腰直角三角形;
(4)先猜想出∠A的度数,则可得∠EDF+∠EFD=120°,根据前面的推导过程知∠EDF+∠EFD=120°时,∠DEF=60°,再由∠B=∠DEF以及等腰三角形的性质继而推得猜想的正确性.
(1)∵AB=AC,
∴∠B=∠C,
∵AD+EC=AB,AB=AD+BD,
∴BD=CE,
在△BDE和△CEF中,
 ,
,
∴△BDE≌△CEF(SAS)
∴DE=EF,
∴△DEF是等腰三角形;
(2)∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
由(1)知△BDE≌△CEF,
则∠BDE=∠CEF,
∴∠DEF=∠B,
∵∠A=40°,
∴∠B=∠C=![]() =70°,
=70°,
∴∠DEF=70°;
(3)△DEF不可能是等腰直角三角形,
∵AB=AC,
∴∠B=∠C≠90°,
由(2)知∠DEF=∠B,
∴∠DEF=∠B≠90°,
∴△DEF不可能是等腰直角三角形;
(4)当∠A=60°时,∠EDF+∠EFD=120°,
理由是:当∠EDF+∠EFD=120°时,
则∠DEF=180°-120°=60°,
∴∠B=∠DEF=60°,
∴∠A=180°-∠B-∠C=180°-60°-60°=60°,
∴当∠A=60°时,∠EDF+∠EFD=120°.
-
科目: 来源: 题型:
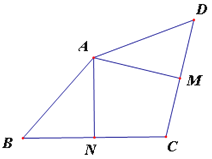
查看答案和解析>>【题目】如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC。
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数
 的图象过点
的图象过点 .
. 求该函数的解析式;
求该函数的解析式; 过点
过点 分别向
分别向 轴和
轴和 轴作垂线,垂足为
轴作垂线,垂足为 和
和 ,求四边形
,求四边形 的面积;
的面积; 求证:过此函数图象上任意一点分别向
求证:过此函数图象上任意一点分别向 轴和
轴和 轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.
轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为4的⊙O中,CD为直径,AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )

A.
 π B.
π B.  π C.
π C.  π D.
π D.  π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长为
 ,宽为
,宽为  的大长方形被分割为
的大长方形被分割为  小块,除阴影
小块,除阴影  ,
, 外,其余
外,其余  块是形状、大小完全相同的小长方形,其较短一边长为
块是形状、大小完全相同的小长方形,其较短一边长为  .
.
(1)每个小长方形较长的一边长是
 (用含
(用含  的代数式表示).
的代数式表示).(2)分别用含
 ,
, 的代数式表示阴影
的代数式表示阴影  ,
, 的面积,并计算阴影 A 的面积与阴影B的面积的差.
的面积,并计算阴影 A 的面积与阴影B的面积的差.(3)当
 时,阴影
时,阴影  与阴影
与阴影  的面积差会随着
的面积差会随着  的变化而变化吗?请你作出判断,并说明理由.
的变化而变化吗?请你作出判断,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的顶角为36°,则这个三角形就是黄金三角形。如图,在△ABC中,BA=BC,D 在边 CB 上,且 DB=DA=AC。

(1)如图1,写出图中所有的黄金三角形,并证明;
(2)若 M为线段 BC上的点,过 M作直线MH⊥AD于 H,分别交直线 AB,AC与点N,E,如图 2,试写出线段 BN、CE、CD之间的数量关系,并加以证明.
相关试题

