【题目】在△ABC中,AB=AC=![]() , BC=2,以AB
, BC=2,以AB![]() 为直径的⊙O分别交AC、BC于点D、E。
为直径的⊙O分别交AC、BC于点D、E。
(1)求证:E是BC的中点;
(2)连结DE,求证:△CDE∽△CBA;
(3)求△CDE的面积.
参考答案:
【答案】
(1)证明:连接AE,
∵AB为⊙O的直径,
∴∠AED=90°,
即AE⊥BC,
又∵AB=AC,
∴E为BC中点.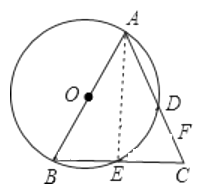
(2)证明:四边形是⊙O的内接四边形,
∴∠BED+∠BAD=180°,
又∵∠BED+∠DEC=180°,
∴∠BAD=∠DEC,
又∵∠BCA=∠DCE,
∴△CDE∽△CBA.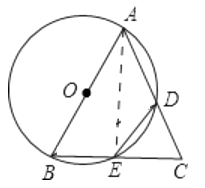
(3)解:由(1)知E为BC中点,
∵BC=2,
∴CE=BE=![]() BC=1,
BC=1,
由(2)知△CDE∽△CBA,
又∵AC=![]() ,
,
∴CE:CA=1:![]() ,
,
∴![]() =
=![]() ,
,
又由(1)知即AE⊥BC,
∴AE=![]() =2,
=2,
∴S△ABC=![]() .BC.AE=
.BC.AE=![]() ×2×2=2,
×2×2=2,
∴S△CDE=![]() S△ABC=
S△ABC=![]() ×2=
×2=![]() .
.
【解析】(1)连接AE,由圆周角定理得出∠AED=90°,又由等腰三角形的性质得出E为BC中点.
(2)由圆的内接四边形和邻补角定义得出∠BAD=∠DEC,又由∠BCA=∠DCE,根据相似三角形的判定:两个对应角相等的三角形相似即可得证.
(3)由(1)知E为BC中点,结合已知得出CE=BE=![]() BC=1,再结合勾股定理得出AE=
BC=1,再结合勾股定理得出AE=![]() =2,又由(2)知△CDE∽△CBA,根据相似三角形的性质得出
=2,又由(2)知△CDE∽△CBA,根据相似三角形的性质得出![]() =
=![]() ,由S△ABC=
,由S△ABC=![]() .BC.AE=
.BC.AE=![]() ×2×2=2,得出S△CDE=
×2×2=2,得出S△CDE=![]() S△ABC=
S△ABC=![]() ×2=
×2=![]() .
.
【考点精析】利用三角形的面积和等腰三角形的性质对题目进行判断即可得到答案,需要熟知三角形的面积=1/2×底×高;等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
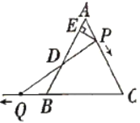
查看答案和解析>>【题目】如图,
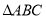 是边长为
是边长为 的等边三角形,
的等边三角形, 是
是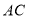 边上一动点,由
边上一动点,由 向
向 运动(与
运动(与 、
、 不重合),
不重合),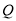 是
是 延长线上一动点,与点
延长线上一动点,与点 同时以相同的速度由
同时以相同的速度由 向
向 延长线方向运动(
延长线方向运动(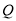 不与
不与 重合),过
重合),过 作
作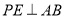 于
于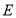 ,连接
,连接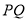 交
交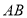 于
于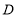 .
.
(1)若
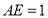 时,求
时,求 的长;
的长;(2)当
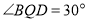 时,求
时,求 的长;
的长;(3)在运动过程中线段
 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段 的长;如果发生变化,请说明理由.
的长;如果发生变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).

A. 8cm B. 10cm C. 11cm D. 12cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月,若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边△ADE,AC、BE相交于点F,则∠EFC为( )

A.135°B.145°C.120°D.165°
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆某著名景区依托天然河道新开发了一款乘船体验项目.小明乘船由甲地顺流而下到乙地,然后由乙地逆流而上到丙地,然后靠岸乘车离开景点.若水流速度为2km/小时,船在静水中的速度为8km/小时.在整个乘船过程中,轮船与甲地相距的路程S(千米)与轮船出发的时间t(小时)之间的关系如图所示,甲乙两地间的距离为_____千米.
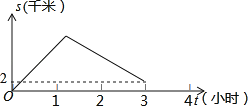
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
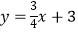 与x轴交于点A,与直线 y=kx-3交于点C(c,6),直线
与x轴交于点A,与直线 y=kx-3交于点C(c,6),直线  与y轴交于点B,连接AB.
与y轴交于点B,连接AB.
(1)求k的值;
(2)求证:∠CAO=∠BAO;
(3)P为OA上一点,连结PB,M为PB中点,延长MO交直线AC于点N,若OP=x, ,求y关于x的函数表达式.
,求y关于x的函数表达式.
相关试题

