【题目】如图,直线 ![]() 与x轴交于点A,与直线 y=kx-3交于点C(c,6),直线
与x轴交于点A,与直线 y=kx-3交于点C(c,6),直线 ![]() 与y轴交于点B,连接AB.
与y轴交于点B,连接AB.
(1)求k的值;
(2)求证:∠CAO=∠BAO;
(3)P为OA上一点,连结PB,M为PB中点,延长MO交直线AC于点N,若OP=x, ![]() ,求y关于x的函数表达式.
,求y关于x的函数表达式.
参考答案:
【答案】
(1)解:∵C(c,6)y=![]() x+3,
x+3,
∴![]() c+3=6,
c+3=6,
∴c=4,
∴C(4,6),
又 ∵ C(4,6)在y=kx-3 上,
∴4k-3=6,
∴k=![]() .
.
(2)证明:∵AC所在直线方程为:y=![]() x+3,
x+3,
∴D(0,3),A(-4,0),
∴AO=4,DO=3,
∴AD=5,
又∵BC所在的直线方程为:y=![]() x-3,
x-3,
∴B(0,-3),
∴BO=3,
∴AB=5,
在△ADO和△ABO中,
∵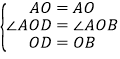 ,
,
∴△ADO≌△ABO,
∴∠CAO=∠BAO.
(3)解:过M作ME⊥OP,作NF⊥y轴,设N(a,![]() a+3),
a+3),
∴Rt△OEM∽Rt△NFO,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴a=![]() ,
,
又∵![]() =y,
=y,
∴![]() =y,
=y,
∴y=![]() .
.
∴y关于x的函数表达式为:y=![]() .
.
【解析】
(1)由待定系数法得出c=4,又 ∵由C(4,6)在y=kx-3 上,得出k的值.
(2)由AC和BC所在直线方程方可得出D(0,3),A(-4,0),B(0,-3);从而可以利用全等三角形的判定SAS得出△ADO≌△ABO,再根据全等三角形的性质得出∠CAO=∠BAO.
(3)过M作ME⊥OP,作NF⊥y轴,设N(a,![]() a+3),根据已知条件可以证明Rt△OEM∽Rt△NFO,再根据相似三角形的性质可以得出
a+3),根据已知条件可以证明Rt△OEM∽Rt△NFO,再根据相似三角形的性质可以得出 ![]() =
=![]() =
=![]() ,从而得出a=
,从而得出a=![]() ,又由
,又由![]() =y,得出y=
=y,得出y=![]() .
.
【考点精析】本题主要考查了确定一次函数的表达式和相似三角形的判定与性质的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC=
 , BC=2,以AB
, BC=2,以AB 为直径的⊙O分别交AC、BC于点D、E。
为直径的⊙O分别交AC、BC于点D、E。
(1)求证:E是BC的中点;
(2)连结DE,求证:△CDE∽△CBA;
(3)求△CDE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边△ADE,AC、BE相交于点F,则∠EFC为( )

A.135°B.145°C.120°D.165°
-
科目: 来源: 题型:
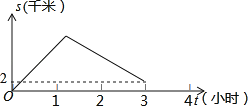
查看答案和解析>>【题目】重庆某著名景区依托天然河道新开发了一款乘船体验项目.小明乘船由甲地顺流而下到乙地,然后由乙地逆流而上到丙地,然后靠岸乘车离开景点.若水流速度为2km/小时,船在静水中的速度为8km/小时.在整个乘船过程中,轮船与甲地相距的路程S(千米)与轮船出发的时间t(小时)之间的关系如图所示,甲乙两地间的距离为_____千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线C:y=
 x2+bx+c 交
x2+bx+c 交  轴于点A(0,-1)且过点
轴于点A(0,-1)且过点  , P是抛物线C上一个动点,过P作PB∥OA,以P为圆心,2为半径的圆交PB于C、D两点(点D位于点C下方).
, P是抛物线C上一个动点,过P作PB∥OA,以P为圆心,2为半径的圆交PB于C、D两点(点D位于点C下方).
(1)求抛物线C的解析式;
(2)连接AP交⊙P于点E,连接DE,AC.若ΔACP是以CP为直角边的直角三角形,求∠EDC的度数;
(3)若当点P经过抛物线C上所有的点后,点D随之经过的路线被直线 截得的线段长为8,求
截得的线段长为8,求 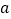 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:有一内角为直角的三角形叫做直角三角形.类似地,我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(4,0),B(-4,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列), BC与经过A,B,D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然△DCE,△DEF,△DAE是半直角三角形.

(1)求证:△ABC是半直角三角形;
(2)求证:∠DEC=∠DEA;
(3)若点D的坐标为(0,8),
①求AE的长;
②记BC与AD的交点为F,求ΔACF与ΔBCA的面积之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,AD∥BC,AC,BD相交于O,则图中能够全等的三角形共有( )对.

A.4B.3C.2D.1
相关试题

