【题目】如图,![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形,![]() 是
是![]() 边上一动点,由
边上一动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合),过
重合),过![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.
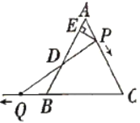
(1)若![]() 时,求
时,求![]() 的长;
的长;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)在运动过程中线段![]() 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段![]() 的长;如果发生变化,请说明理由.
的长;如果发生变化,请说明理由.
参考答案:
【答案】(1)2(2)2(3)DE=3为定值,理由见解析
【解析】
(1)根据等边三角形的性质得到∠A=60![]() ,根据三角形内角和定理得到∠APE=30
,根据三角形内角和定理得到∠APE=30![]() ,根据直角三角形的性质计算;
,根据直角三角形的性质计算;
(2)过P作PF∥QC,证明△DBQ≌△DFP,根据全等三角形的性质计算即可;
(3)根据等边三角形的性质、直角三角形的性质解答.
(1)∵△ABC是等边三角形,
∴∠A=60![]() ,
,
∵PE⊥AB,
∴∠APE=30![]() ,
,
∵AE=1,∠APE=30![]() ,PE⊥AB,
,PE⊥AB,
∴AP=2AE=2;
(2)解:过P作PF∥QC,
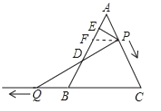
则△AFP是等边三角形,
∵P、Q同时出发,速度相同,即BQ=AP,
∴BQ=PF,
在△DBQ和△DFP中,
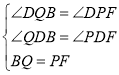 ,
,
∴△DBQ≌△DFP,
∴BD=DF,
∵∠BQD=∠BDQ=∠FDP=∠FPD=30![]() ,
,
∴BD=DF=FA=![]() AB=2,
AB=2,
∴AP=2;
(3)解:由(2)知BD=DF,
∵△AFP是等边三角形,PE⊥AB,
∴AE=EF,
∴DE=DF+EF=![]() BF+
BF+![]() FA=
FA=![]() AB=3为定值,即DE的长不变.
AB=3为定值,即DE的长不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一项工程,在工程招标时,接到甲、乙两个工程队的投标书,施工一天,需付甲工程队工程款
 万元,乙工程队工程款
万元,乙工程队工程款 万元,工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:①甲队单独完成这项工程刚好如期完成;②乙队单独完成这项工程要比规定日期多用
万元,工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:①甲队单独完成这项工程刚好如期完成;②乙队单独完成这项工程要比规定日期多用 天;③若甲乙两队合作
天;③若甲乙两队合作 天,余下的工程由乙队单独也正好如期完成.
天,余下的工程由乙队单独也正好如期完成.(1)甲、乙单独完成各需要多少天?
(2)在不耽误工期的情况下,你觉得那一种施工方案最节省工程款?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解题过程,然后解答后面两个问题.
解方程:|x-3|=2.
解:当x-3≥0时,原方程可化为x-3=2,解得x=5;
当x-3<0时,原方程可化为x-3=-2,解得x=1.
所以原方程的解是x=5或x=1.
(1)解方程:|3x-2|-4=0.
(2)解关于x的方程:|x-2|=b+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角板按图①所示的位置放置,图②是由它抽象画出的几何图形,
 ,
, ,
, ,
, ,
, ,
, 在同一条直线上,连接
在同一条直线上,连接 .
.(1)请找出图②中与
 全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)求证:
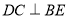 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).

A. 8cm B. 10cm C. 11cm D. 12cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月,若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC=
 , BC=2,以AB
, BC=2,以AB 为直径的⊙O分别交AC、BC于点D、E。
为直径的⊙O分别交AC、BC于点D、E。
(1)求证:E是BC的中点;
(2)连结DE,求证:△CDE∽△CBA;
(3)求△CDE的面积.
相关试题

