【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月,若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
参考答案:
【答案】(1)甲,乙两种型号设备每台的价格分别为12万元和10万元;(2)有6种购买方案;(3)最省钱的购买方案为选购甲型设备4台,乙型设备6台
【解析】
(1)设甲,乙两种型号设备每台的价格分别为![]() 万元和
万元和![]() 万元,根据购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元,列出方程组,然后求解即可;
万元,根据购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元,列出方程组,然后求解即可;
(2)设购买甲型设备![]() 台,乙型设备
台,乙型设备![]() 台,根据公司经预算决定购买节省能源的新设备的资金不超过110万元,列出不等式,然后求解即可得出购买方案;
台,根据公司经预算决定购买节省能源的新设备的资金不超过110万元,列出不等式,然后求解即可得出购买方案;
(3)根据甲型设备的产量为![]() 吨/月,乙型设备的产量为
吨/月,乙型设备的产量为![]() 吨/月和总产量不低于
吨/月和总产量不低于![]() 吨,列出不等式,求出
吨,列出不等式,求出![]() 的取值范围,再根据每台的钱数,即可得出最省钱的购买方案.
的取值范围,再根据每台的钱数,即可得出最省钱的购买方案.
解:(1)设甲,乙两种型号设备每台的价格分别为![]() 万元和
万元和![]() 万元
万元
由题意得:![]() ,
,
解得:![]() ,
,
则甲,乙两种型号设备每台的价格分别为12万元和10万元.
(2)设购买甲型设备![]() 台,乙型设备
台,乙型设备![]() 台,
台,
则:![]() ,
,
∴![]() ,
,
∵![]() 取非负整数
取非负整数
∴![]()
∴有6种购买方案.
(3)由题意:![]()
∴![]()
∴![]() 为4或5.
为4或5.
当![]() 时,购买资金为:
时,购买资金为:![]() (万元),
(万元),
当![]() 时,购买资金为:
时,购买资金为:![]() (万元),
(万元),
则最省钱的购买方案为,选购甲型设备4台,乙型设备6台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角板按图①所示的位置放置,图②是由它抽象画出的几何图形,
 ,
, ,
, ,
, ,
, ,
, 在同一条直线上,连接
在同一条直线上,连接 .
.(1)请找出图②中与
 全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)求证:
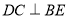 .
.
-
科目: 来源: 题型:
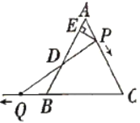
查看答案和解析>>【题目】如图,
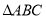 是边长为
是边长为 的等边三角形,
的等边三角形, 是
是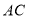 边上一动点,由
边上一动点,由 向
向 运动(与
运动(与 、
、 不重合),
不重合),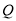 是
是 延长线上一动点,与点
延长线上一动点,与点 同时以相同的速度由
同时以相同的速度由 向
向 延长线方向运动(
延长线方向运动(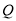 不与
不与 重合),过
重合),过 作
作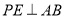 于
于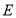 ,连接
,连接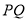 交
交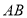 于
于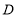 .
.
(1)若
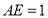 时,求
时,求 的长;
的长;(2)当
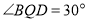 时,求
时,求 的长;
的长;(3)在运动过程中线段
 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段 的长;如果发生变化,请说明理由.
的长;如果发生变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).

A. 8cm B. 10cm C. 11cm D. 12cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC=
 , BC=2,以AB
, BC=2,以AB 为直径的⊙O分别交AC、BC于点D、E。
为直径的⊙O分别交AC、BC于点D、E。
(1)求证:E是BC的中点;
(2)连结DE,求证:△CDE∽△CBA;
(3)求△CDE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边△ADE,AC、BE相交于点F,则∠EFC为( )

A.135°B.145°C.120°D.165°
-
科目: 来源: 题型:
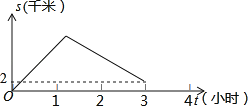
查看答案和解析>>【题目】重庆某著名景区依托天然河道新开发了一款乘船体验项目.小明乘船由甲地顺流而下到乙地,然后由乙地逆流而上到丙地,然后靠岸乘车离开景点.若水流速度为2km/小时,船在静水中的速度为8km/小时.在整个乘船过程中,轮船与甲地相距的路程S(千米)与轮船出发的时间t(小时)之间的关系如图所示,甲乙两地间的距离为_____千米.
相关试题

