搜索
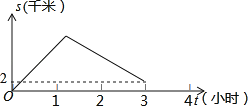
【题目】重庆某著名景区依托天然河道新开发了一款乘船体验项目．小明乘船由甲地顺流而下到乙地，然后由乙地逆流而上到丙地，然后靠岸乘车离开景点．若水流速度为2km/小时，船在静水中的速度为8km/小时．在整个乘船过程中，轮船与甲地相距的路程S（千米）与轮船出发的时间t（小时）之间的关系如图所示，甲乙两地间的距离为_____千米．
参考答案：
【答案】12.5或10．
【解析】
需分类讨论：（1）丙在甲地和乙地之间，（2）丙不在甲地和乙地之间，设甲乙两地距离为x，即可解题．
解：根据图形可知甲、丙两地间的距离为2km．
（1）丙在甲地和乙地之间，设甲乙两地距离为x，
则
，
解得：x＝12.5．
（2）丙不在甲地和乙地之间，设甲乙两地距离为x，
则
，
解得：x＝10．
∴甲乙两地间的距离为12.5km或10km．
故答案为：12.5或10.
-
科目： 来源： 题型：
查看答案和解析>>【题目】每年的6月5日为世界环保日，为了提倡低碳环保，某公司决定购买10台节省能源的新设备，现有甲、乙两种型号的设备可供选购，经调查：购买3台甲型设备比购买2台乙型设备多花16万元，购买2台甲型设备比购买3台乙型设备少花6万元．
（1）求甲、乙两种型号设备的价格；
（2）该公司经预算决定购买节省能源的新设备的资金不超过110万元，你认为该公司有哪几种购买方案；
（3）在（2）的条件下，已知甲型设备的产量为240吨/月，乙型设备的产量为180吨/月，若每月要求总产量不低于2040吨，为了节约资金，请你为该公司设计一种最省钱的购买方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=AC=
， BC=2，以AB
为直径的⊙O分别交AC、BC于点D、E。
（1）求证：E是BC的中点；
（2）连结DE，求证：△CDE∽△CBA；
（3）求△CDE的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD的外侧，作等边△ADE，AC、BE相交于点F，则∠EFC为（ ）
A.135°B.145°C.120°D.165°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
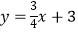与x轴交于点A，与直线 y=kx-3交于点C（c,6），直线 
与y轴交于点B，连接AB．
（1）求k的值；
（2）求证：∠CAO=∠BAO；
（3）P为OA上一点，连结PB，M为PB中点，延长MO交直线AC于点N，若OP=x，
,求y关于x的函数表达式． -
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线C：y=
x2+bx+c 交 
轴于点A（0，-1）且过点 
， P是抛物线C上一个动点，过P作PB∥OA，以P为圆心，2为半径的圆交PB于C、D两点（点D位于点C下方）．
（1）求抛物线C的解析式；
（2）连接AP交⊙P于点E，连接DE，AC．若ΔACP是以CP为直角边的直角三角形，求∠EDC的度数；
（3）若当点P经过抛物线C上所有的点后，点D随之经过的路线被直线
截得的线段长为8，求 
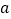的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】我们知道：有一内角为直角的三角形叫做直角三角形．类似地，我们定义：有一内角为45°的三角形叫做半直角三角形．如图，在平面直角坐标系中，O为原点，A（4，0），B（－4，0），D是y轴上的一个动点，∠ADC=90°(A、D、C按顺时针方向排列)， BC与经过A，B，D三点的⊙M交于点E，DE平分∠ADC，连结AE，BD．显然△DCE，△DEF，△DAE是半直角三角形．
（1）求证：△ABC是半直角三角形；
（2）求证：∠DEC=∠DEA；
（3）若点D的坐标为（0，8），
①求AE的长；
②记BC与AD的交点为F，求ΔACF与ΔBCA的面积之比．
相关试题
