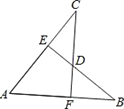
【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④CF是AB的垂直平分线.以上结论正确的有( )个.
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】C
【解析】
由∠A=∠A,AB=AC,∠B=∠C,可推出①选项正确;由AE=AF,AD=AD可知②正确;由∠B=∠C,BF=CE,可证得△BDF≌△CDE,得到③正确;而点F不一定是AB的中点,故④错误.
:∵BE⊥AC于E,CF⊥AB于F,
∴∠AFC=∠AEB=90°,故在Rt△AEB中,∠B=90°-∠A,在Rt△AFC中∠C=90°-∠A,
∴∠B=∠C,
在△ABE和△ACF中,
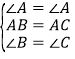 ,
,
∴△ABE≌△ACF(ASA),
故①选项正确,
由AE=AF,AC=AB,得BF=CE,
在△BDF和△CDE中,
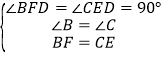 ,
,
∴△BDF≌△CDE,选项②正确,
∵△ABE≌△ACF,
∴AE=AF,AC=AB,
连接AD,
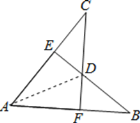
在Rt△AFD和Rt△AED中,
![]() ,
,
∴Rt△AFD≌Rt△AED(HL),
∴∠DAF=∠DAE,即点D在∠BAC的平分线上,选项③正确,
而点F不一定是AB的中点,故④错误.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=50° ,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)若AB=4,求
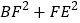 的值.
的值.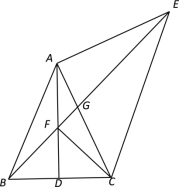
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
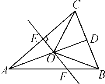
A. 3对 B. 4对 C. 5对 D. 6对
-
科目: 来源: 题型:
查看答案和解析>>【题目】A厂一月份产值为16万元,因管理不善,二、三月份产值的月平均下降率为x(0<x<1).B厂一月份产值为12万元,二月份产值下降率为x,经过技术革新,三月份产值增长,增长率为2x.三月份A、B两厂产值分别为yA、yB(单位:万元).
(1)分别写出yA、yB与x的函数表达式;
(2)当yA=yB时,求x的值;
(3)当x为何值时,三月份A、B两厂产值的差距最大?最大值是多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠BAC=90°,∠BAD=30°,AD=AE,则∠EDC的度数是______.
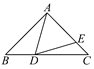
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,点D、E分别在AC、BC上,且CDBC=ACCE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB、BC分别交于点F、G.
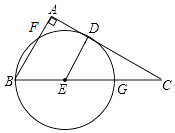
(1)求证:AC是⊙E的切线.
(2)若AF=4,CG=5,求⊙E的半径;
(3)若Rt△ABC的内切圆圆心为I,则IE= .
相关试题

