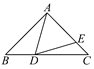
【题目】如图,在等腰直角△ABC中,∠BAC=90°,∠BAD=30°,AD=AE,则∠EDC的度数是______.
参考答案:
【答案】15°
【解析】
由△ABC为等腰直角三角形,可得∠B=45°,已知∠BAD=30°,得∠DAE=90°-30°=60°,又AD=AE,则△ADE为等边三角形,∠ADE=60°,由外角的性质可求∠EDC的度数.
∵在△ABC中,∠BAC=90°,AB=AC,
∴∠B=45°,
又∵∠BAD=30°,
∴∠DAE=90°-30°=60°,
而AD=AE,∴△ADE为等边三角形,则∠ADE=60°,
又∵∠EDC+∠ADE=∠B+∠BAD(外角定理),
即∠EDC=45°+30°-60°=15°.
故答案为:15°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
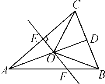
A. 3对 B. 4对 C. 5对 D. 6对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④CF是AB的垂直平分线.以上结论正确的有( )个.
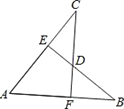
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】A厂一月份产值为16万元,因管理不善,二、三月份产值的月平均下降率为x(0<x<1).B厂一月份产值为12万元,二月份产值下降率为x,经过技术革新,三月份产值增长,增长率为2x.三月份A、B两厂产值分别为yA、yB(单位:万元).
(1)分别写出yA、yB与x的函数表达式;
(2)当yA=yB时,求x的值;
(3)当x为何值时,三月份A、B两厂产值的差距最大?最大值是多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,点D、E分别在AC、BC上,且CDBC=ACCE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB、BC分别交于点F、G.
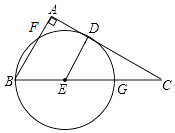
(1)求证:AC是⊙E的切线.
(2)若AF=4,CG=5,求⊙E的半径;
(3)若Rt△ABC的内切圆圆心为I,则IE= . -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,D为BC边上一点.

(1)如图①,在Rt△ABC中,∠C=90°,将△ABC沿着AD折叠,点C落在AB边上.请用直尺和圆规作出点D(不写作法,保留作图痕迹);
(2)如图②,将△ABC沿着过点D的直线折叠,点C落在AB边上的E处.
①若DE⊥AB,垂足为E,请用直尺和圆规作出点D(不写作法,保留作图痕迹);
②若AB=4 ,BC=6,∠B=45°,则CD的取值范围是 .
,BC=6,∠B=45°,则CD的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称
单价(元)
数量(个)
金额(元)
挂钟
30
2
60
垃圾桶
15
塑料鞋架
40
艺术饰品
a
2
90
电热水壶
35
1
b
合计
8
280
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
相关试题

