【题目】在平面直角坐标系xOy中,将任意两点P(x1,y1)与Q(x2,y2)之间的“直距”定义为:DPQ=|x1﹣x2|+|y1﹣y2|.
例如:点M(1,﹣2),点N(3,﹣5),则DMN=|1﹣3|+|﹣2﹣(﹣5)|=5.已知点A(1,0)、点B(﹣1,4).
(1)则DAO= ,DBO= ;
(2)如果直线AB上存在点C,使得DCO为2,请你求出点C的坐标;
(3)如果⊙B的半径为3,点E为⊙B上一点,请你直接写出DEO的取值范围.

参考答案:
【答案】(1)1;5;(2)(0,2)或(![]() ,﹣
,﹣![]() );(3)4﹣2
);(3)4﹣2![]() ≤DEO≤5+3
≤DEO≤5+3![]() .
.
【解析】
(1)根据“直距”定义结合点A、B的坐标,即可求出结论;
(2)根据点A、B的坐标,利用待定系数法求出直线AB的解析式,设点C的坐标为(m,-2m+2),根据DCO=2,即可得出关于m的含绝对值符号的一元一次方程,解之即可得出结论;
(3)设点E的坐标为(x,y),则当点E在第一象限时,DEO=x+y,当点E在第二象限时,DEO=y-x.作直线y=x、y=-x的平行线(与),找出这些平行线与y轴交点的纵坐标的最值即可得出结论.
(1)DAO=|1-0|+|0-0|=1;DBO=|-1-0|+|4-0|=5.
故答案为:1;5.
(2)设直线AB的解析式为y=kx+b(k≠0),
将点A(1,0)、B(-1,4)代入y=kx+b,
![]() ,解得:
,解得:![]() ,
,
∴直线AB的解析式为y=-2x+2.
设点C的坐标为(m,-2m+2),
∵DCO=2,
∴|m-0|+|-2m+2-0|=2,
解得:m1=0,m2=![]() ,
,
∴点C的坐标为(0,2)或(![]() ,-
,-![]() ).
).
(3)∵点B的坐标为(-1,4),⊙B的半径为3,
∴⊙B位于第一、二象限,
设点E的坐标为(x,y),
∴当点E在第一象限时,DEO=x+y,当点E在第二象限时,DEO=y-x.
设⊙B与y轴交于点N(下面的交点),连接BN,过点B作BM⊥y轴于点M,
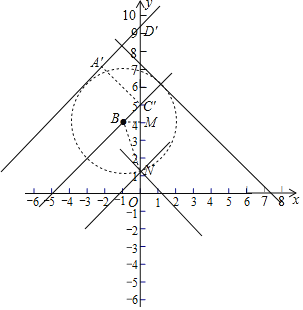
在Rt△BMN中,BM=1,BN=3,
∴MN=![]() ,
,
∴ON=4-2![]() ;
;
设直线y=x+b经过点B,
∵点B的坐标为(-1,4),
∴4=-1+b,解得:b=5,
∴点C′的坐标为(0,5).
过点C′作A′D′⊥直线A′D′与点A′,则A′C′=3,
又∵△A′C′D′为等腰直角三角形,
∴C′D′=3![]() ,
,
∴OD′=5+3![]() .
.
∴4-2![]() ≤DEO≤5+3
≤DEO≤5+3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是___.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,两组对边分别平行的四边形叫做平行四边形。平行四边形的内角和、外角和都等于360°,根据三角形的学习经验,请你再写出平行四边形的两条性质;并证明其中一条性质
(1)______________________________________________
(2)________________________________________________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E是BC边上的一个动点,连接AE,将线段AE绕点A逆时针旋转90°,得到AF,连接EF,交对角线BD于点G,连接AG.
(1)根据题意补全图形;
(2)判定AG与EF的位置关系并证明;
(3)当AB=3,BE=2时,求线段BG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE.

(1)如图1,过F点作FD⊥AC交AC于D点,求证:EC+CD=DF;
(2)如图2,连接BF交AC于G点,若
 =3,求证:E点为BC中点;
=3,求证:E点为BC中点;(3)当E点在射线CB上,连接BF与直线AC交于G点,若
 ,则
,则 =_______
=_______ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象如图所示,它与
的图象如图所示,它与 轴的两个交点分别为
轴的两个交点分别为 ,
, .对于下列命题:①
.对于下列命题:① ;②
;② ;③
;③ ;④
;④ .其中正确的有( )
.其中正确的有( )
A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度
 米,顶点
米,顶点 距水面
距水面 米(即
米(即 米),小孔顶点
米),小孔顶点 距水面
距水面 米(即
米(即 米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,则此时大孔的水面宽度
米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,则此时大孔的水面宽度 长为( )
长为( )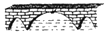

A.
 米 B.
米 B.  C.
C.  米 D.
米 D.  米
米
相关试题

