搜索
【题目】为了响应政府“绿色出行”的号召，李华选择骑自行车到郊外游玩，她离家的距离与时间的关系如图所示，请根据图像回答下列问题.
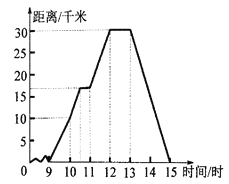
（1）李华到达离家最远的地方是几时？此时离家多远？
（2）李华返回时的速度是多少？
（3）李华全程骑车的平均速度是多少？
参考答案：
【答案】（1）（1）李华到达离家最远的地方是在12时，此时离家30千米；（2）李华返回的途中速度为：
千米/小时；（3）李华全程骑车的平均速度为：
千米/小时.
【解析】
（1）利用图中的点的横坐标表示时间，纵坐标表示离家的距离，进而得出答案；
（2）用离家的距离除以所用时间即可；
（3）用李华全程所行的路程除以所用的时间即可．
观察图象可知：
（1）李华到达离家最远的地方是在12时，此时离家30千米；
（2）李华返回的途中速度为：
千米/小时；
（3）李华全程骑车的平均速度为：
千米/小时.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABD和△ACE中，AB=AD，AC=AE，∠BAD=∠CAE，连接BC、DE相交于点F，BC与AD相交于点G．
（1）试判断线段BC、DE的数量关系，并说明理由；
（2）若BC平分∠ABD，求证线段FD是线段FG 和 FB的比例中项.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点D恰好为BC的中点，过点D作⊙O的切线交AC边于点F.
（1）求证：DF⊥AC；
（2）若∠ABC=30°，求tan∠BCO的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABC中，AB=AC=6
，∠BAC=90°，点D、E为BC边上的两点，分别沿AD、AE折叠，B、C两点重合于点F，若DE=5，则AD的长为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，现有一个均匀的转盘被平均分成6等份，分别标有数字2、3、4、5、6、7这六个数字，转动转盘，当转盘停止时，指针指向的数字即为转出的数字.求：
（1）转动转盘，转出的数字大于3的概率是多少？
（2）现有两张分别写有3和4的卡片，要随机转动转盘，转盘停止后记下转出的数字，与两张卡片上的数字分别作为三条线段的长度.这三条线段能构成三角形的概率是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在Rt△ABC中，∠C=90°，P是BC边上不同于B、C的一动点，过P作PQ⊥AB，垂足为Q，连接AP．
（1）试说明不论点P在BC边上何处时，都有△PBQ与△ABC相似；
（2）若Rt△AQP≌Rt△ACP≌Rt△BQP，求tanB的值；
（3）已知AC=3，BC=4，当BP为何值时，△AQP面积最大，并求出最大值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y＝ax2＋bx＋c与x轴交于A、B两点，与y轴交于点C， D为OC的中点，直线AD交抛物线于点E（2，6），且△ABE与△ABC的面积之比为3∶2．
（1）求这条抛物线对应的函数关系式；
（2）连结BD，试判断BD与AD的位置关系，并说明理由；
（3）连结BC交直线AD于点M，在直线AD上，是否存在这样的点N（不与点M重合），使得以A、B、N为顶点的三角形与△ABM相似？若存在，请求出点N的坐标；若不存在，请说明理由．
相关试题
