【题目】在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.

(1)试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似;
(2)若Rt△AQP≌Rt△ACP≌Rt△BQP,求tanB的值;
(3)已知AC=3,BC=4,当BP为何值时,△AQP面积最大,并求出最大值.
参考答案:
【答案】(1)证明见解析;(2)![]() ; (3)当BP=
; (3)当BP=![]() 时,△APQ的面积最大,最大值是
时,△APQ的面积最大,最大值是![]() ;
;
【解析】试题分析:(1)直接证明∠C=∠PQB=90°,而∠B=∠B,即可根据两角对应相等的两三角形相似;
(2)分别根据全等三角形的性质,求出AQ=QB=AC,然后根据锐角三角形函数的性质求出tanB的值;
(3)利用勾股定理求出AB的值,然后根据相似三角形的性质列出比例式求出PQ、BQ,再根据三角形的面积公式求出△AQP面积,根据二次函数的性质和配方法解答即可.
试题解析:(1)不论点P在BC边上何处时,都有
∠PQB=∠C=90°,∠B=∠B
∴△PBQ∽△ABC;
(2)∵Rt△AQP≌Rt△ACP∴AQ=AC
又Rt△AQP≌Rt△BQP ∴AQ=QB
∴AQ=QB=AC
∴∠B=![]()
∴![]()
(3)设BP=x(0<x<4),由勾股定理,得 AB=5
∵由(1)知,△PBQ∽△ABC,
∴![]() ,即
,即 ![]() ∴
∴![]()
![]()
S△APQ=![]() =
=![]() =
=![]()
∴当![]() 时,△APQ的面积最大,最大值是
时,△APQ的面积最大,最大值是![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABC中,AB=AC=6
 ,∠BAC=90°,点D、E为BC边上的两点,分别沿AD、AE折叠,B、C两点重合于点F,若DE=5,则AD的长为_____.
,∠BAC=90°,点D、E为BC边上的两点,分别沿AD、AE折叠,B、C两点重合于点F,若DE=5,则AD的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应政府“绿色出行”的号召,李华选择骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图像回答下列问题.
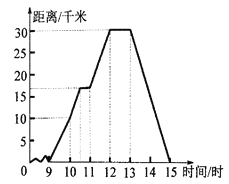
(1)李华到达离家最远的地方是几时?此时离家多远?
(2)李华返回时的速度是多少?
(3)李华全程骑车的平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.求:

(1)转动转盘,转出的数字大于3的概率是多少?
(2)现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.这三条线段能构成三角形的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C, D为OC的中点,直线AD交抛物线于点E(2,6),且△ABE与△ABC的面积之比为3∶2.

(1)求这条抛物线对应的函数关系式;
(2)连结BD,试判断BD与AD的位置关系,并说明理由;
(3)连结BC交直线AD于点M,在直线AD上,是否存在这样的点N(不与点M重合),使得以A、B、N为顶点的三角形与△ABM相似?若存在,请求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块矩形纸板,长为20cm,宽为14cm,在它的四角各切去一个同样的正方形,然后将四周突出部分沿虚线折起,就能制作一个无盖的长方体盒子,如果这个无盖的长方体底面积为160cm2,那么该长方体盒子体积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批小家电,平均每天可售出20台,每台盈利40元.为了去库存,商场决定采取适当的降价措施.经调查发现,在一定范围内,小家电的单价每降5元,商场平均每天可多售出10台.
(1)若将这批小家电的单价降低x元,则每天的销售量是______台(用含x的代数式表示);
(2)如果商场通过销售这批小家电每天要盈利1250元,那么单价应降多少元?
(3)若这批小家电的单价有三种降价方式:降价10元、降价20元、降价30元,如果你是商场经理,你准备采取哪种降价方式?说说理由.
相关试题

