【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据. 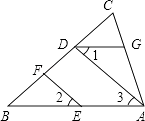
【解】∵EF∥AD(已知)
∴∠2=()
又∵∠1=∠2(已知)
∴∠1=∠3(等式性质或等量代换)
∴AB∥()
∴∠BAC+=180°()
又∵∠BAC=70°(已知)
∴∠AGD=110°(等式性质)
参考答案:
【答案】∠3;两直线平行,同位角相等;DG;内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补
【解析】解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠1=∠3(等式性质或等量代换)
∴AB∥DG(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补)
又∵∠BAC=70°(已知)
∴∠AGD=110°(等式性质)
所以答案是:∠3,两直线平行,同位角相等;DG,内错角相等,两直线平行;∠AGD,两直线平行,同旁内角互补.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设平面内一点到等边三角形中心的距离为d,等边三角形的内切圆半径为r,外接圆半径为R .对于一个点与等边三角形,给出如下定义:满足r≤d≤R的点叫做等边三角形的中心关联点.在平面直角坐标系xOy中,等边△ABC的三个顶点的坐标分别为A(0,2),B(﹣
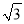 ,﹣1),C(
,﹣1),C(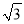 ,﹣1).
,﹣1).(1)已知点D(2,2),E(
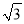 ,1),F(
,1),F(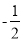 ,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;
,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;(2)如图1,过点A作直线交x轴正半轴于M,使∠AMO=30°.
①若线段AM上存在等边△ABC的中心关联点P(m,n),求m的取值范围;
②将直线AM向下平移得到直线y=kx+b,当b满足什么条件时,直线y=kx+b上总存在等边△ABC的中心关联点;(直接写出答案,不需过程)
(3)如图2,点Q为直线y=﹣1上一动点,⊙Q的半径为
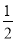 .当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
.当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
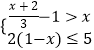 ,并把其解集在数轴上表示出来.
,并把其解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是( )
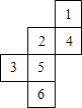
A.3
B.6
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
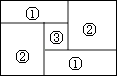
A.①②
B.②③
C.①③
D.①②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=6,ab=4,则a2+b2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点D、E、F分别是等边△ABC的三条边AB、BC、CA上的点.
(1)如图(1),若ED⊥AB,DF⊥AC,FE⊥BC,求证:△DEF是等边三角形;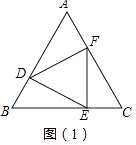
(2)如图(2),若AD=BE=CF,求证:△DEF是等边三角形;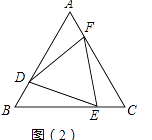
(3)如图(3),若△DEF是等边三角形,求证:AD=BE=CF.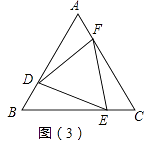
相关试题

