【题目】解不等式组: 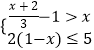 ,并把其解集在数轴上表示出来.
,并把其解集在数轴上表示出来.
参考答案:
【答案】解: 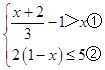 ,
,
由①得:x<﹣ ![]() ,
,
由②得:x≥﹣ ![]() ,
,
不等式组的解集为:﹣ ![]() ≤x<﹣
≤x<﹣ ![]() ,
,
在数轴上表示为:
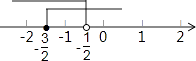 .
.
【解析】首先分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集即可.
【考点精析】利用不等式的解集在数轴上的表示和一元一次不等式组的解法对题目进行判断即可得到答案,需要熟知不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).
-
科目: 来源: 题型:
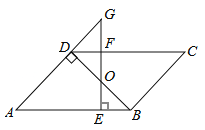
查看答案和解析>>【题目】如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷两枚质地均匀的正方体骰子1次,下列事件中是不可能事件的是( )
A.朝上的点数之和为13
B.朝上的点数之和为12
C.朝上的点数之和为2
D.朝上的点数之和小于3 -
科目: 来源: 题型:
查看答案和解析>>【题目】设平面内一点到等边三角形中心的距离为d,等边三角形的内切圆半径为r,外接圆半径为R .对于一个点与等边三角形,给出如下定义:满足r≤d≤R的点叫做等边三角形的中心关联点.在平面直角坐标系xOy中,等边△ABC的三个顶点的坐标分别为A(0,2),B(﹣
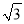 ,﹣1),C(
,﹣1),C(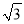 ,﹣1).
,﹣1).(1)已知点D(2,2),E(
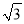 ,1),F(
,1),F(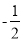 ,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;
,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;(2)如图1,过点A作直线交x轴正半轴于M,使∠AMO=30°.
①若线段AM上存在等边△ABC的中心关联点P(m,n),求m的取值范围;
②将直线AM向下平移得到直线y=kx+b,当b满足什么条件时,直线y=kx+b上总存在等边△ABC的中心关联点;(直接写出答案,不需过程)
(3)如图2,点Q为直线y=﹣1上一动点,⊙Q的半径为
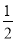 .当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
.当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是( )
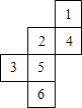
A.3
B.6
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.
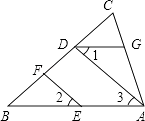
【解】∵EF∥AD(已知)
∴∠2=()
又∵∠1=∠2(已知)
∴∠1=∠3(等式性质或等量代换)
∴AB∥()
∴∠BAC+=180°()
又∵∠BAC=70°(已知)
∴∠AGD=110°(等式性质) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
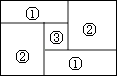
A.①②
B.②③
C.①③
D.①②③
相关试题

