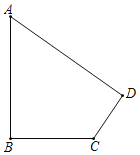
【题目】如图,已知一块四边形的草地ABCD,其中∠B=90°,AB=20m,BC=15m,CD=7m,DA=24m,求这块草地的面积.
参考答案:
【答案】234m2.
【解析】
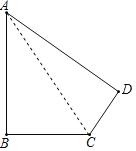
仔细分析题目,需要求得四边形的面积才能求得结果.连接AC,由AD、CD、AC的长度关系可得△ACD为一直角三角形,AC为斜边;由此看,四边形ABCD由Rt△ACD和Rt△ABC构成,则容易求解.
解:如图,连接AC,如图所示.
∵∠B=90°,AB=20m,BC=15m,
∴AC=![]() =
=![]() =25m.
=25m.
∵AC=25m,CD=7m,AD=24m,
∴AD2+DC2=AC2,
∴△ACD是直角三角形,且∠ADC=90°,
∴S△ABC=![]() ×AB×BC=
×AB×BC=![]() ×20×15=150m2,S△ACD=
×20×15=150m2,S△ACD=![]() ×CD×AD=
×CD×AD=![]() ×7×24=84m2,
×7×24=84m2,
∴S四边形ABCD=S△ABC+S△ACD=234m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】寒假即将到来,外出旅游的人数逐渐增多,对旅行包的需求也将增多,某店准备到生产厂家购买旅行包,该厂有甲、乙两种新型旅行包.若购进10个甲种旅行包和20个乙种旅行包共需5600元,若购进20个甲种旅行包和10个乙种旅行包共需5200元.
(1)甲、乙两种旅行包的进价分别是多少元?
(2)若该店恰好用了7000元购买旅行包;
①设该店购买了m个甲种旅行包,求该店购买乙种旅行包的个数;
②若该店将甲种旅行包的售价定为298元,乙种旅行包的售价定为325元,则当该店怎么样进货,才能获得最大利润,并求出最大利润.
-
科目: 来源: 题型:
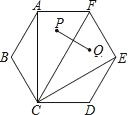
查看答案和解析>>【题目】如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )
A. 1 B. 2 C. 2
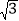 ﹣2 D. 4﹣2
﹣2 D. 4﹣2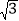
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式了的平方,如3+2
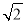 =(1+
=(1+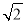 )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:若设a+b
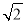 =(m+n
=(m+n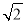 )2=m2+2n2+2mn
)2=m2+2n2+2mn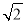 (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),则有a=m2+2n2,b=2mn.
这样小明就找到了一种把类似a+b
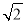 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)若a+b
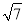 =(m+n
=(m+n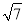 )2,当a、b、m、n均为整数时,用含m、n的式子分别表示a、b,得:a= ,b= ;
)2,当a、b、m、n均为整数时,用含m、n的式子分别表示a、b,得:a= ,b= ;(2)若a+6
 =(m+n
=(m+n )2,且a、m、n均为正整数,求a的值;
)2,且a、m、n均为正整数,求a的值;(3)化简:
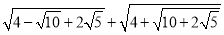 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.人体构造学的研究成果表明,一般情况下人的指距
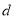 和身高
和身高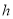 成如下所示的关系.
成如下所示的关系.
(1)直接写出身高
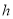 与指距
与指距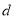 的函数关系式: .
的函数关系式: .(2)姚明的身高是226厘米,可预测他的指距约为多少?(精确到0.1厘米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的正半轴相交于A,B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC.有下列结论:①abc<0;②3b+4c<0;③c>﹣1;④关于x的方程ax2+bx+c=0有一个根为﹣
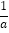 ,其中正确的结论个数是( )
,其中正确的结论个数是( )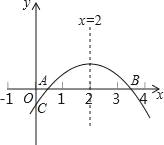
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
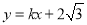 与
与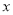 轴、
轴、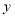 轴分别相交于点
轴分别相交于点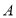 、点
、点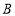 ,
,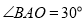 ,若将
,若将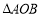 沿直线
沿直线 折叠,使点
折叠,使点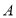 与点
与点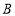 重合,折痕
重合,折痕 与
与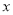 轴交于点
轴交于点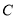 ,与
,与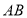 交于点
交于点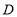 .
.(1)求
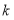 的值;
的值;(2)求点
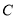 的坐标;
的坐标;(3)求直线
 的表达式.
的表达式.
相关试题

