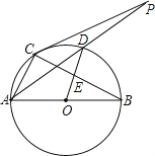
【题目】 如图,圆O是以AB为直径的△ABC的外接圆,D是劣弧![]() 的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
(1)求证:OE=![]() AC;
AC;
(2)求证:![]() ;
;
(3)当AC=6,AB=10时,求切线PC的长.
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)PC=15.
【解析】
(1)由于D是![]() 的中点,利用垂径定理的推论,可证OD⊥BC,而AC⊥BC,故OD∥AC,又O是AB中点,利用平行线分线段成比例定理的推论,可得BE:CE=OB:OA,从而可知E是BC中点,即OE是△ABC的中位线,利用三角形中位线定理可证OE=
的中点,利用垂径定理的推论,可证OD⊥BC,而AC⊥BC,故OD∥AC,又O是AB中点,利用平行线分线段成比例定理的推论,可得BE:CE=OB:OA,从而可知E是BC中点,即OE是△ABC的中位线,利用三角形中位线定理可证OE=![]() AC;
AC;
(2)连接CD,连接CO并延长交圆O于点F,连接DF,先证明∠PCD=∠CAP,再利用两组角对应相等,证明△PCD∽△PAC,得出![]() ,结合CD=BD利用等式性质可证;
,结合CD=BD利用等式性质可证;
(3)连接BD,由AC=6,AB=10,利用勾股定理可求BC,进而求出BE、OE、DE,再利用勾股定理可求BD2、AD2,从而解出AD、BD、CD,结合(2)中的结论,利用比例性质,可求出DP、AP,那么可求CP2,从而求出CP.
(1)证明:∵AB为直径,
∴∠ACB=90°,
∴AC⊥BC,
又D为![]() 中点,
中点,
∴OD⊥BC,OD∥AC,
又O为AB中点,
∴E为BC的中点,即OE为△ABC的中位线,
∴![]() ;
;
(2)证明:连接CD,
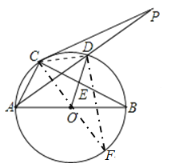
连接CO并延长交圆O于点F,连接DF,
∵PC为切线,
∴∠PCD+∠DCO==90°,∠DCO+∠F=90°,
∴∠PCD=∠F,又∠F=∠CAP,
∴∠PCD=∠CAP,
又∠P为公共角,
∴△PCD∽△PAC,
∴![]() ,
,
∴![]()
又CD=BD,
∴![]() ;
;
(3)解:连接BD,∵AC=6,AB=10,

∴BC=8,BE=4,OE=3,
∴DE=2,
∴BD2=DE2+BE2=20,∴BD=2![]() ,
,
∴AD2=AB2-BD2=80,∴AD=4![]() ,
,
∴AD=4![]() ,
,
又D为![]() 中点,∴CD=BD=2
中点,∴CD=BD=2![]() ,
,
由(2)![]() ,
,
∴![]() ,
,
由(1)中△PCD∽△PAC得,
∴CP2=DPAP=![]() ,
,
∴PC=15.
-
科目: 来源: 题型:
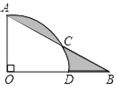
查看答案和解析>>【题目】如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点A、点C,交OB于点D,若OA=3,则阴影都分的面积为___________.
-
科目: 来源: 题型:
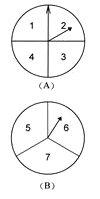
查看答案和解析>>【题目】甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜.
(1)用列表法(或画树状图)求甲获胜的概率;
(2)你认为这个游戏规则对双方公平吗?请简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】扶贫工作小组对果农进行精准扶贫,帮助果农将一种有机生态水果拓宽了市场.与去年相比,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了1元,批发销售总额比去年增加了
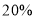 .
.(1)已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元?
(2)某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克,设水果店一天的利润为
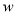 元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.) -
科目: 来源: 题型:
查看答案和解析>>【题目】某市场将进货价为40元/件的商品按60元/件售出,每星期可卖出300件.市场调查反映:如调整价格,每涨价1元/件,每星期该商品要少卖出10件.
(1)请写出该商场每月卖出该商品所获得的利润y(元)与该商品每件涨价x(元)间的函数关系式;
(2)每月该商场销售该种商品获利能否达到6300元?请说明理由;
(3)请分析并回答每件售价在什么范围内,该商场获得的月利润不低于6160元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.
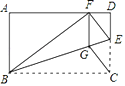
(1)求证:四边形CEFG是菱形;
(2)若AB=6,AD=10,求四边形CEFG的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
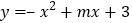 与
与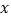 轴的一个交点
轴的一个交点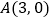 .
.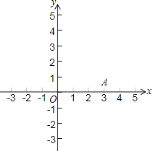
(1)试分别求出这条抛物线与
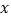 轴的另一个交点
轴的另一个交点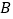 及与
及与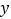 轴的交点
轴的交点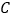 的坐标.
的坐标.(2)设抛物线的顶点为
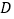 ,请在图中画出抛物线的草图,若点
,请在图中画出抛物线的草图,若点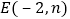 在直线
在直线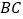 上,试判断
上,试判断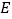 点是否在经过
点是否在经过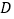 点的反比例函数的图象上,并说明理由;
点的反比例函数的图象上,并说明理由;(3)试求
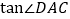 的值.
的值.
相关试题

