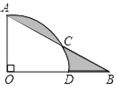
【题目】如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点A、点C,交OB于点D,若OA=3,则阴影都分的面积为___________.
参考答案:
【答案】![]()
【解析】
连接OC,作CH⊥OB于H,根据直角三角形的性质求出AB,根据勾股定理求出BD,证明△AOC为等边三角形,得到∠AOC=60°,∠COB=30°,根据扇形面积公式、三角形面积公式计算即可.
连接OC,作CH⊥OB于H,
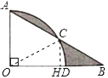
∵∠AOB=90°,∠B=30°,
∴∠OAB=60°,AB=2OA=6,
由勾股定理得,OB=![]() ,
,
∵OA=OC,∠OAB=60°,
∴△AOC为等边三角形,
∴∠AOC=60°,
∴∠COB=30°,
∴CO=CB,CH=![]() OC=
OC=![]() ,
,
∴阴影部分的面积=![]() =
=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内,给定不在同一条直线上的点
 (如图所示),点
(如图所示),点 到点
到点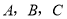 的距离均等于
的距离均等于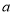 (
(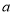 为常数),到点
为常数),到点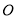 的距离等于
的距离等于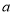 的所有点组成图形
的所有点组成图形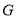 ,
,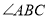 的平分线交图形
的平分线交图形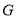 于点
于点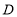 ,连接
,连接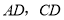 .
.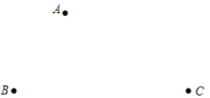
(1)求证:
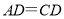 ;
;(2)过点
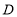 作
作 ,垂足为
,垂足为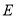 ,作
,作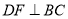 ,垂足为
,垂足为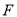 ,延长
,延长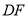 交图形
交图形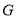 于点
于点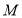 ,连接
,连接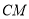 .若
.若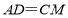 ,求直线
,求直线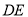 与图形
与图形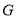 的公共点个数.
的公共点个数. -
科目: 来源: 题型:
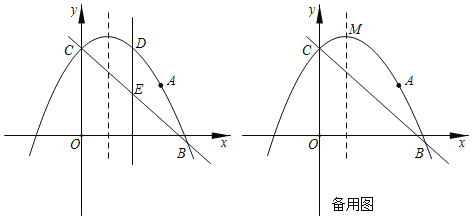
查看答案和解析>>【题目】如图,抛物线
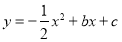 过点
过点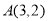 ,且与直线
,且与直线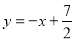 交于B、C两点,点B的坐标为
交于B、C两点,点B的坐标为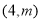 .
.
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线
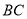 上方的一点,过点D作
上方的一点,过点D作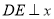 轴交直线
轴交直线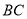 于点E,点P为对称轴上一动点,当线段
于点E,点P为对称轴上一动点,当线段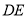 的长度最大时,求
的长度最大时,求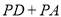 的最小值;
的最小值;(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使
 ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明从如图所示的二次函数
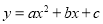 的图象中,观察得出了下面五条信息:①c>0,②abc<0,③a-b+c>0,④
的图象中,观察得出了下面五条信息:①c>0,②abc<0,③a-b+c>0,④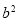 >4ac,⑤2a=-2b,其中正确结论是( ).
>4ac,⑤2a=-2b,其中正确结论是( ).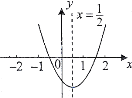
A.①②④B.②③④C.③④⑤D.①③⑤
-
科目: 来源: 题型:
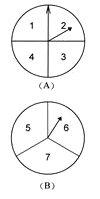
查看答案和解析>>【题目】甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜.
(1)用列表法(或画树状图)求甲获胜的概率;
(2)你认为这个游戏规则对双方公平吗?请简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】扶贫工作小组对果农进行精准扶贫,帮助果农将一种有机生态水果拓宽了市场.与去年相比,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了1元,批发销售总额比去年增加了
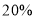 .
.(1)已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元?
(2)某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克,设水果店一天的利润为
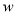 元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.) -
科目: 来源: 题型:
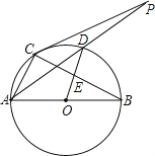
查看答案和解析>>【题目】 如图,圆O是以AB为直径的△ABC的外接圆,D是劣弧
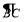 的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;(1)求证:OE=
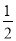 AC;
AC;(2)求证:
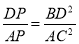 ;
;(3)当AC=6,AB=10时,求切线PC的长.
相关试题

