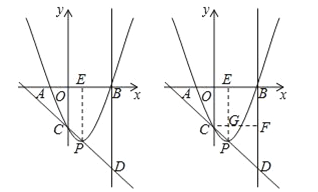
【题目】已知二次函数![]() (a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3.
(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3.

(1)求A、B两点的坐标;
(2)若tan∠PDB=![]() ,求这个二次函数的关系式.
,求这个二次函数的关系式.
参考答案:
【答案】(1)A(![]() ,0);(2)
,0);(2)![]() .
.
【解析】
试题分析:(1)由二次函数的解析式可求出对称轴为x=1,过点P作PE⊥x轴于点E,所以OE:EB=CP:PD;
(2)过点C作CF⊥BD于点F,交PE于点G,构造直角三角形CDF,利用tan∠PDB=![]() 即可求出FD,由于△CPG∽△CDF,所以可求出PG的长度,进而求出a的值,最后将A(或B)的坐标代入解析式即可求出c的值.
即可求出FD,由于△CPG∽△CDF,所以可求出PG的长度,进而求出a的值,最后将A(或B)的坐标代入解析式即可求出c的值.
试题解析:(1)过点P作PE⊥x轴于点E,∵![]() ,∴该二次函数的对称轴为:x=1,∴OE=1,∵OC∥BD,∴CP:PD=OE:EB,∴OE:EB=2:3,∴EB=
,∴该二次函数的对称轴为:x=1,∴OE=1,∵OC∥BD,∴CP:PD=OE:EB,∴OE:EB=2:3,∴EB=![]() ,∴OB=OE+EB=
,∴OB=OE+EB=![]() ,∴B(
,∴B(![]() ,0).∵A与B关于直线x=1对称,∴A(
,0).∵A与B关于直线x=1对称,∴A(![]() ,0);
,0);
(2)过点C作CF⊥BD于点F,交PE于点G,令x=1代入![]() ,∴y=c﹣a,令x=0代入
,∴y=c﹣a,令x=0代入![]() ,∴y=c,∴PG=a,∵CF=OB=
,∴y=c,∴PG=a,∵CF=OB=![]() ,∴tan∠PDB=
,∴tan∠PDB=![]() ,∴FD=2,∵PG∥BD,∴△CPG∽△CDF,∴
,∴FD=2,∵PG∥BD,∴△CPG∽△CDF,∴![]() ,∴PG=
,∴PG=![]() ,∴a=
,∴a=![]() ,∴
,∴![]() ,把A(
,把A(![]() ,0)代入
,0)代入![]() ,∴解得:c=﹣1,∴该二次函数解析式为:
,∴解得:c=﹣1,∴该二次函数解析式为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副含30°和45°角的三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm(如图1),点G为边BC(EF)的中点,边FD与AB相交于点H,此时线段BH的长是____.现将三角板DEF绕点G按顺时针方向旋转(如图2),在∠CGF从0°到60°的变化过程中,点H相应移动的路径长共为_________.(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
 .
.(1)写出此二次函数图象的对称轴;
(2)在如图中建立平面直角坐标系,并画出该函数的图象.(列表、描点、连线)
(3)结合图象回答问题:
①当x的取值范围是 时,y≤0?
②将此抛物线向 平移 个单位时,它与x轴有且只有一个公共点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量
 的取值范围;
的取值范围;(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是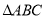 的外接圆,
的外接圆,  点在
点在 边上,
边上, 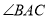 的平分线交
的平分线交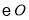 于点
于点 ,连接
,连接 ,过点
,过点 作
作 的平行线,与
的平行线,与 的延长线相交于点
的延长线相交于点 .
.(1)求证:
 是
是 的切线;
的切线;(2)求证:△PBD∽△DCA;
(3)当
 时,求线段
时,求线段 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.
计时制:0.05元/分;
包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
相关试题

