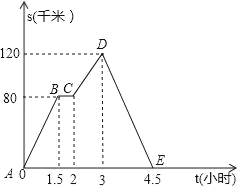
【题目】如下图中的图象(折线ABCDE)描述了一汽车在某一直路上的行驶过程中,汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
①汽车在途中停留了0.5小时;
②汽车行驶3小时后离出发地最远;
③汽车共行驶了120千米;
④汽车返回时的速度是80千米/小时.
其中正确的说法共有( )
A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】C
【解析】
根据函数图像与描述即可进行判断.
①汽车在途中停留了2-1.5=0.5小时,正确;
②汽车行驶3小时后离出发地最远,正确;
③汽车共行驶了120+120=240千米,故错误;
④汽车返回时的速度是120÷(4.5-3)=80千米/小时,正确.
故正确的个数为3,故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本
(1)求每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
-
科目: 来源: 题型:
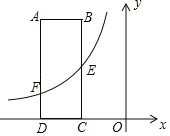
查看答案和解析>>【题目】如图,在直角坐标系
 中,矩形
中,矩形 的
的 边在
边在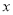 轴上,
轴上, 点坐标为
点坐标为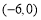 边
边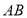 、
、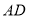 的长分别为3、8,
的长分别为3、8,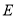 是
是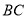 的中点,反比例函数
的中点,反比例函数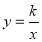 的图象经过点
的图象经过点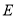 ,与
,与 边交于点
边交于点 .
.
(1)求
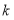 的值及经过
的值及经过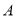 、
、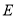 两点的一次函数的表达式;
两点的一次函数的表达式;(2)若
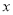 轴上有一点
轴上有一点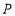 ,使
,使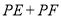 的值最小,试求出点
的值最小,试求出点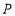 的坐标;
的坐标;(3)在(2)的条件下,连接
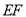 、
、 、
、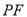 ,在直线
,在直线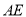 上找一点
上找一点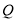 ,使得
,使得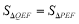 直接写出符合条件的
直接写出符合条件的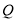 点坐标.
点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y1=
 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.

-
科目: 来源: 题型:
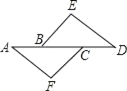
查看答案和解析>>【题目】如图所示,A、B、C、D在同一直线上,AB=CD,DE∥AF,若要使△ACF≌△DBE,则还需要补充一个条件:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3,E,F 分别是AB,BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y1=
 的图象与函数y2=kx+b的图象交于点A(﹣1,a)B(﹣8+a,1)
的图象与函数y2=kx+b的图象交于点A(﹣1,a)B(﹣8+a,1)
(1)求函数y=
 和y=kx+b的表达式;
和y=kx+b的表达式;(2)观察图象,直接写出不等式
 <kx+b的解.
<kx+b的解.
相关试题

