【题目】如图,函数y1=![]() 的图象与函数y2=kx+b的图象交于点A(﹣1,a)B(﹣8+a,1)
的图象与函数y2=kx+b的图象交于点A(﹣1,a)B(﹣8+a,1)

(1)求函数y=![]() 和y=kx+b的表达式;
和y=kx+b的表达式;
(2)观察图象,直接写出不等式![]() <kx+b的解.
<kx+b的解.
参考答案:
【答案】(1)y1=﹣![]() ,y=x+5;(2)﹣4<x<﹣1或x>0.
,y=x+5;(2)﹣4<x<﹣1或x>0.
【解析】
(1)根据反比例函数系数k的几何意义得出﹣1×a=(﹣8+a)×1=m,可求出a的值,得到A、B的坐标,进一步即得反比例函数解析式,然后利用待定系数法求一次函数解析式;
(2)根据交点坐标结合图象即可求得.
解:(1)∵函数y1=![]() 的图象经过点A(﹣1,a)、B(﹣8+a,1),
的图象经过点A(﹣1,a)、B(﹣8+a,1),
∴﹣1×a=(﹣8+a)×1=m,
∴a=4,m=﹣4,
∴A(﹣1,4),B(﹣4,1),
∴反比例函数解析式为y1=﹣![]() ,
,
把A(﹣1,4),B(﹣4,1)代入y2=kx+b得![]() ,
,
解得k=1,b=5,
∴一次函数解析式为y=x+5;
(2)由图象可知:不等式![]() <kx+b的解为﹣4<x<﹣1或x>0.
<kx+b的解为﹣4<x<﹣1或x>0.
-
科目: 来源: 题型:
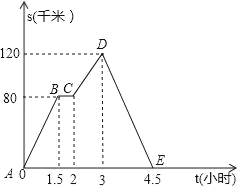
查看答案和解析>>【题目】如下图中的图象(折线ABCDE)描述了一汽车在某一直路上的行驶过程中,汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
①汽车在途中停留了0.5小时;
②汽车行驶3小时后离出发地最远;
③汽车共行驶了120千米;
④汽车返回时的速度是80千米/小时.
其中正确的说法共有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
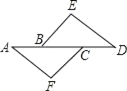
查看答案和解析>>【题目】如图所示,A、B、C、D在同一直线上,AB=CD,DE∥AF,若要使△ACF≌△DBE,则还需要补充一个条件:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3,E,F 分别是AB,BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.

-
科目: 来源: 题型:
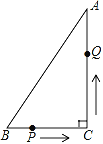
查看答案和解析>>【题目】如图,在Rt△ABC中,AC=24cm,BC=7cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
(1)当t为何值时,P、Q两点的距离为5
 cm?
cm?(2)当t为何值时,△PCQ的面积为15cm2?
(3)请用配方法说明,点P运动多少时间时,四边形BPQA的面积最小?最小面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两公司为“见义勇为基金会”各捐款3000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐20元.请你根据上述信息,就这两个公司的“人数”或“人均捐款”提出一个用分式方程解决的题,并写出解题过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(
 )﹣2﹣(﹣2)0+(﹣0.2)2018×(﹣5)2018;
)﹣2﹣(﹣2)0+(﹣0.2)2018×(﹣5)2018;(2)用整式乘法公式计算:1012﹣1;
(3)(x2y+2x2y﹣y3)÷y﹣(y+2x)(2x﹣y);
(4)先化简,再求值:(a﹣2b)2+(a﹣b)(a+b)﹣2(a﹣3b)(a﹣b),其中,a=1,b=﹣2.
相关试题

