【题目】如图,将![]() 的长方形纸片
的长方形纸片![]() 沿过项点
沿过项点![]() 的直线
的直线![]() 为折痕折叠时,点
为折痕折叠时,点![]() 与边
与边![]() 上的点
上的点![]() 重合,试分别求出
重合,试分别求出![]() 的长.
的长.

参考答案:
【答案】DQ=6;PQ=5.
【解析】
由折叠的性质可知△ABP≌AQP,根据全等三角形的性质可知AB=AQ=10,利用勾股定理即可求出线段DQ的长度;由DQ=6,得出CQ=DC-DQ=4,设PQ=x,则PB=PQ=x,所以CP=BC-BP=8-x,利用勾股定理可建立关于x的方程,解方程求出x的值即可.
解:由折叠的性质可知△ABP≌AQP,
∴AB=AQ=10,
∵四边形ABCD是矩形,
∴∠D=90°,
∵AD=8cm,
∴![]() ,
,
∴线段DQ的长度是6cm;
由(1)可知DQ=6,
∴CQ=DC-DQ=4,
设PQ=x,则PB=PQ=x,
∴CP=BC-BP=8-x,
∴x2=42+(8-x)2,
解得:x=5,
∴线段PQ的长度是5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师对试卷讲评课中九年级学生参与的深度与广度进行评价调查,每位学生最终评价结果为主动质疑、独立思考、专注听讲、讲解题目四项中的一项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:


(1)在这次评价中,一共抽查了名学生;
(2)在扇形统计图中,项目“主动质疑”所在扇形的圆心角度数为度;
(3)请将频数分布直方图补充完整;
(4)如果全市九年级学生有8000名,那么在试卷评讲课中,“独立思考”的九年级学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了争创全国文明卫生城市,优化城市环境,某市公交公司决定购买10辆全新的混合动力公交车,现有
 两种型号,它们的价格及年省油量如下表:
两种型号,它们的价格及年省油量如下表:型 号


价格(万元/辆)
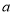

年省油量(万升/辆)
2.4
2
经调查,购买一辆
 型车比购买一辆
型车比购买一辆 型车多20万元,购买2辆
型车多20万元,购买2辆 型车比购买3辆
型车比购买3辆 型车少60万元.
型车少60万元.(1)请求出
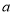 和
和 的值;
的值;(2)若购买这批混合动力公交车(两种车型都要有), 每年能节省的油量不低于22.4万升,请问有几种购车方案?(不用一一列出)请求出最省钱的购车方案所需的车款.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,点
,点 分别在射线
分别在射线 上移动,
上移动, 的平分线与
的平分线与 的外角平分线交于点
的外角平分线交于点 .
.
(1)当
 时,
时,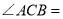 .
.(2)请你猜想:随着
 两点的移动,
两点的移动, 的度数大小是否变化?请说明理由.
的度数大小是否变化?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从2007年4月18日零点起,铁路将实施第六次大提速,届时“子弹头”动力组列车的速度将大大提高.若有一普通列车长为140米,“子弹头”动力组列车长为110米,两列车若同向而行,两车交汇的时间为9秒,若两列车相向而行,两车交汇的时间为3秒,求“子弹头”动力组列车和普通列车的速度分别为多少?若设“子弹头”动力组列车的速度为x米/秒,普通列车速度为y米/秒,则可列出方程组为( )
A.
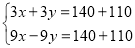 B.
B. 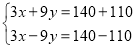
C.
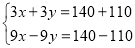 D.
D. 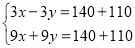
相关试题

