【题目】问题背景:(1)已知A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出这几个点,并分别找到线段AB和CD中点P1、P2,然后写出它们的坐标,则P1 ,P2 .
探究发现:(2)结合上述计算结果,你能发现若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为 .
拓展应用:(3)利用上述规律解决下列问题:已知三点E(﹣1,2),F(3,1),G(1,4),第四个点H(x,y)与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.

参考答案:
【答案】(1)(2,2),(﹣1,﹣2);(2)![]() ;(3)(1,﹣1)或(5,3)或(﹣3,5)
;(3)(1,﹣1)或(5,3)或(﹣3,5)
【解析】
(1)根据坐标的确定方法直接描点,分别读出各点的纵横坐标,即可得到各中点的坐标;
(2)根据(1)中的坐标与中点坐标找到规律;
(3)利用(2)中的规律进行分类讨论即可答题.
(1)如图:A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出它们如下:
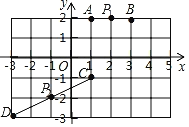
线段AB和CD中点P1、P2的坐标分别为(2,2)、(﹣1,﹣2)
故答案为:(2,2)、(﹣1,﹣2).
(2)若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为(![]() ,
,![]() ).
).
故答案为:![]() .
.
(3)∵E(﹣1,2),F(3,1),G(1,4),
∴EF、FG、EG的中点分别为:(1,![]() )、(2,
)、(2,![]() )、(0,3)
)、(0,3)
∴①HG过EF中点(1,![]() )时,
)时,![]() =1,
=1,![]() =
=![]()
解得:x=1,y=﹣1,故H(1,﹣1);
②EH过FG中点(2,![]() )时,
)时,![]() =2,
=2,![]() =
=![]()
解得:x=5,y=3,故H(5,3);
③FH过EG的中点(0,3)时,![]() =0,
=0,![]() =3
=3
解得:x=﹣3,y=5,故H(﹣3,5).
∴点H的坐标为:(1,﹣1)或(5,3)或(﹣3,5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列不等式化为“x>a”或“x<a”的形式:
(1)2x>3x-4;
(2)5x-1<14;
(3)-
 x<-3;
x<-3;(4)
 x<
x< x+1.
x+1. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )

A.600﹣250 米
米
B.600 ﹣250米
﹣250米
C.350+350 米
米
D.500 米
米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为 .
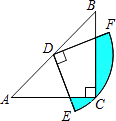
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动3个单位长度到达点A1 , 第二次将点A1向右移动6个单位长度到达点A2 , 第三次将点A2向左移动9个单位长度到达点A3 , 则A3表示的数是按照这种移动规律移动下去,第n次移动到点AN , 如果点AN与原点的距离不小于20,那么n的最小值是 .
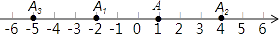
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题3tan30°﹣|﹣2|+
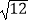 +(﹣1)2017;
+(﹣1)2017;
(1)计算:3tan30°﹣|﹣2|+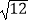 +(﹣1)2017;
+(﹣1)2017;
(2)解方程: =
= 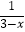 ﹣2.
﹣2. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2015)0+|1﹣
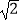 |﹣2cos45°+
|﹣2cos45°+ 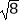 +(﹣
+(﹣  )﹣2 .
)﹣2 .
相关试题

