【题目】将下列不等式化为“x>a”或“x<a”的形式:
(1)2x>3x-4;
(2)5x-1<14;
(3)-![]() x<-3;
x<-3;
(4) ![]() x<
x<![]() x+1.
x+1.
参考答案:
【答案】(1) x<4;(2) x<3; (3) x>27;(4) x>-6.
【解析】
(1)先根据不等式的性质1两边都减去3x,合并同类项后,再根据不等式的性质3两边都除以-1;
(2)先根据不等式的性质1两边都加1,合并同类项后,再根据不等式的性质2两边都除以5;
(3)先根据不等式的性质3两边都乘以-9即可;
(4)先根据不等式的性质1两边都减去![]() x,合并同类项后,再根据不等式的性质2两边都除以6.
x,合并同类项后,再根据不等式的性质2两边都除以6.
(1) ∵2x>3x-4,
∴2x-3x>-4,
∴-x>-4,
∴x<4;
(2) ∵5x-1<14,
∴5x<14+1,
∴5x<15,
∴x<3;
(3)-![]() x<-3,
x<-3,
∴-![]() x×(-9)>-3×(-9)
x×(-9)>-3×(-9)
∴x>27;
(4) ∵ ![]() x<
x<![]() x+1,
x+1,
∴![]() x-
x-![]() x<1,
x<1,
∴-![]() x<1,
x<1,
∴x>-6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)判断下列未知数的值是不是方程2x2+x-1=0的根.
x1=-1,x2=1,x3=
 .
.(2)已知m是方程x2-x-2=0的一个根,求代数式m2-m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市上网有两种收费方案,用户可任选其一,A为计时制--1元
 时;B为包月制--80元
时;B为包月制--80元 月,此外每种上网方式都附加通讯费
月,此外每种上网方式都附加通讯费 元
元 时.
时. 某用户每月上网40小时,选哪种方式比较合适?
某用户每月上网40小时,选哪种方式比较合适? 某用户每月有100元钱用于上网,选哪种方式比较合算?
某用户每月有100元钱用于上网,选哪种方式比较合算? 请你设计一个方案,使用户能合理地选择上网方式.
请你设计一个方案,使用户能合理地选择上网方式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点D是
 上一点,且∠BDE=∠CBE,BD与AE交于点F.
上一点,且∠BDE=∠CBE,BD与AE交于点F. 
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DFDB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长和⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )

A.600﹣250 米
米
B.600 ﹣250米
﹣250米
C.350+350 米
米
D.500 米
米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为 .
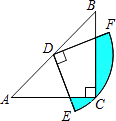
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:(1)已知A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出这几个点,并分别找到线段AB和CD中点P1、P2,然后写出它们的坐标,则P1 ,P2 .
探究发现:(2)结合上述计算结果,你能发现若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为 .
拓展应用:(3)利用上述规律解决下列问题:已知三点E(﹣1,2),F(3,1),G(1,4),第四个点H(x,y)与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.

相关试题

