搜索
【题目】计算题3tan30°﹣|﹣2|+ 
+（﹣1）2017；
（1）计算：3tan30°﹣|﹣2|+ +（﹣1）2017；
（2）解方程： 
= 
﹣2．
参考答案：
【答案】
（1）解：原式= 
﹣2+2 ﹣1=3 ﹣3
（2）解：方程的两边同乘（x﹣3），得：2﹣x=﹣1﹣2（x﹣3），
解得：x=3，
检验：把x=3代入（x﹣3）=0，即x=3是增根，
则原方程无解
【解析】（1）利用特殊锐角三角函数值，绝对值，二次根式的化简，（-1）2007=-1，分别进行化简，再按照实数的运算法则进行计算；
（2）先去分母把分式方程转换为整式方程，解整式方程求出x的值，检验即可。
【考点精析】掌握去分母法和特殊角的三角函数值是解答本题的根本，需要知道先约后乘公分母，整式方程转化出．特殊情况可换元，去掉分母是出路．求得解后要验根，原留增舍别含糊；分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”．
-
科目： 来源： 题型：
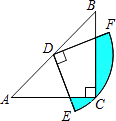
查看答案和解析>>【题目】如图，在△ABC中，CA=CB，∠ACB=90°，AB=2，点D为AB的中点，以点D为圆心作圆心角为90°的扇形DEF，点C恰在弧EF上，则图中阴影部分的面积为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题背景：（1）已知A(1，2)，B(3，2)，C(1，﹣1)，D(﹣3，﹣3)．在平面直角坐标系中描出这几个点，并分别找到线段AB和CD中点P1、P2，然后写出它们的坐标，则P1 ，P2 ．
探究发现：（2）结合上述计算结果，你能发现若线段的两个端点的坐标分别为(x1，y1)，(x2，y2)，则线段的中点坐标为 ．
拓展应用：（3）利用上述规律解决下列问题：已知三点E(﹣1，2)，F(3，1)，G(1，4)，第四个点H(x，y)与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合，求点H的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在数轴上，点A表示1，现将点A沿x轴做如下移动，第一次点A向左移动3个单位长度到达点A1 ， 第二次将点A1向右移动6个单位长度到达点A2 ， 第三次将点A2向左移动9个单位长度到达点A3 ， 则A3表示的数是按照这种移动规律移动下去，第n次移动到点AN ， 如果点AN与原点的距离不小于20，那么n的最小值是 ．
-
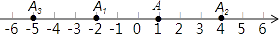
科目： 来源： 题型：
查看答案和解析>>【题目】计算：（﹣2015）0+|1﹣
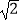|﹣2cos45°+ 
+（﹣ 
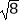）﹣2 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了解今年初四学生的数学学习情况，某校在第一轮模拟测试后，对初四全体同学的数学成绩作了统计分析，绘制如下图表：请结合图表所给出的信息解答系列问题：
成绩
频数
频率
优秀
45
b
良好
a
0.3
合格
105
0.35
不合格
60
c
（1）该校初四学生共有多少人？
（2）求表中a，b，c的值，并补全条形统计图．
（3）初四（一）班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍，求恰好选中甲、乙两位同学的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，AB=CD，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连接AF，CE，若DE=BF，则下列结论：①CF=AE；②OE=OF；③四边形ABCD是平行四边形；④图中共有四对全等三角形．其中正确结论的个数是
A．4 B．3 C．2 D．1
相关试题
