【题目】如图,![]() 的半径为
的半径为![]() ,点
,点![]() 是
是![]() 外的一点,
外的一点,![]() ,点
,点![]() 是
是![]() 上的一个动点,连接
上的一个动点,连接![]() ,直线
,直线![]() 垂直平分
垂直平分![]() ,当直线
,当直线![]() 与
与![]() 相切时,
相切时,![]() 的长度为( )
的长度为( )

A. 10 B. ![]() C. 11 D.
C. 11 D. ![]()
参考答案:
【答案】B
【解析】
连接OA、OC(C为切点),过点O作OB⊥AP.根据题意可知四边形BOCD为矩形,从而可知:BP=8+x,设AB的长为x,在Rt△AOB和Rt△OBP中,由勾股定理列出关于x的方程解得x的长,从而可计算出PA的长度.
如图所示.连接OA、OC(C为切点),过点O作OB⊥AP.

设AB的长为x,在Rt△AOB中,OB2=OA2-AB2=16-x2,
∵l与圆相切,
∴OC⊥l.
∵∠OBD=∠OCD=∠CDB=90°,
∴四边形BOCD为矩形.
∴BD=OC=4.
∵直线l垂直平分PA,
∴PD=BD+AB=4+x.
∴PB=8+x.
在Rt△OBP中,OP2=OB2+PB2,即16-x2+(8+x)2=102,解得x=![]() .
.
PA=2AD=2×(![]() +4)=
+4)= ![]() .
.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知:如图1,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥BF.
(2)如图2所示,△ABC的顶点分别为A(﹣4,5),B(﹣3,2),C(4,﹣1)
①作出△ABC关于x轴对称的图形△A1B1C1;
②用三角板作出△ABC的AB边上的高CH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.

(1)若AB∥x轴,如图1,求t的值;
(2)设点A关于x轴的对称点为A′,连接A′B,在点P运动的过程中,∠OA′B的度数是否会发生变化,若不变,请求出∠OA′B的度数,若改变,请说明理由.
(3)如图2,当t=3时,坐标平面内有一点M(不与A重合)使得以M、P、B为顶点的三角形和△ABP全等,请直接写出点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,以
,以 为直径的
为直径的 分别交
分别交 、
、 两边于点
两边于点 、
、 ,则
,则 的面积为( )
的面积为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )

A.
 是等边三角形
是等边三角形B. 连接
 ,则
,则 分别平分
分别平分 和
和
C. 整个图形是轴对称图形,但不是中心对称图形
D. 四边形
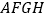 与四边形
与四边形 的面积相等
的面积相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若六边形
 是
是 的内接正六边形,则
的内接正六边形,则 ________,
________, ________,
________, ________,
________, ________.
________.
相关试题

