Question

【题目】如图，在中，，，以为直径的分别交、两边于点、，则的面积为（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】

连接AE．根据圆周角定理易知AE⊥BC；

由于△ABC是等腰△，根据等腰三角形三线合一的性质知E是BC的中点，即CE=BE=1．

在Rt△ABE中，根据勾股定理即可求出AE的长，进而可求出△ABC的面积．

根据圆内接四边形的外角等于内对角，可得出△CDE和△CBA的两组对应角相等，由此可判定两个三角形相似，已知了CE、AC的长，也就知道了两个三角形的相似比，根据相似三角形的面积比等于相似比的平方即可求得△CDE的面积．

连接AE，则AE⊥BC．

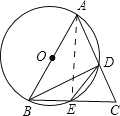
又∵AB=AC，

∴E是BC的中点，即BE=EC=1．

Rt△ABE中，AB=，BE=1，

由勾股定理得：AE=2．

∴S△ABC=BCAE=2．

∵四边形ABED内接于⊙O，

∴∠CDE=∠CBA，∠CED=∠CAB，

∴△CDE∽△CBA，

∴S△CDE：S△ABC=CE2：AC2=1：5．

∴S△CDE=S△ABC=．

故选A．