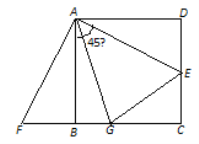
【题目】如图,已知正方形ABCD的边长是2,E是DC上一点,△ADE经顺时针旋转后与△ABF重合.
(1)指出旋转的中心和旋转的角度;
(2)如果连结EF,那么△AEF是怎样的三角形?请说明理由.
(3)已知点G在BC上,且∠GAE=45°.
① 试说明GE=DE+BG.
② 若E是DC的中点,求BG的长.
参考答案:
【答案】(1)旋转的中心是点A,旋转的角度是90°(2)△AEF是等腰直角三角形(3)①证明见解析② BG=![]()
【解析】试题分析:(1)根据正方形的性质得到AB=AD,∠BAD=90°,然后利用旋转的定义得到当△ADE经顺时针旋转后与△ABF重合时,可确定旋转的中心和旋转的角度;
(2)由(1)得到△ADE绕着点A逆时针旋转90°后与△ABF重合,根据旋转的性质得∠FAE=90°,AF=AE,由此可判断△AEF是等腰直角三角形;
(3)①首先得出AG是线段EF的垂直平分线,进而得出DE+GB=BF+BG=GF,即可得出答案;
②首先设GB=x,则GC=2-x,GE=1+x.在Rt△ECG中,∠C=90°,由勾股定理,得1+(2-x)2=(1+x)2,求出x即可.
试题解析:(1)∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴当△ADE经顺时针旋转后与△ABF重合时,旋转的中心是点A,旋转的角度是90°;
(2)△AEF是等腰三角形,理由:
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴△ADE绕点A顺时针旋转90°后与△ABF重合,
∴△ADE≌△ABF,
∴AE=AF,
又∵∠EAF=90°,
∴△AEF是等腰三角形;
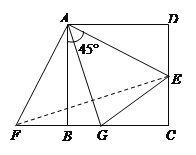
(3)①∵ ∠GAE=45°,∠EAF=90°,
∴ AG是∠EAF的平分线,
又∵ AF=AE,
∴ AG是线段EF的垂直平分线,
∴ GE=GF.
∵ DE=BF,
∴ DE+GB=BF+BG=GF,
∴ GE=DE+BG;
② ∵ E是DC的中点,
∴ DE=EC=FB=1,
设GB=x,则GC=2-x,GE=1+x,
在Rt△ECG中,∠C=90°,由勾股定理,得
1+(2-x)2=(1+x)2,
解这个方程,得x=![]() ,
,
即:BG=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:a3a=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A1(-1,1),A2(2,4),A3(-3,9),A4(4,16),…,用你发现的规律确定点A9的坐标为____.
-
科目: 来源: 题型:
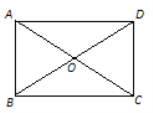
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC、BD相交于O,且AC=2AB.
(1)你能说明△AOB是等边三角形吗?请写出理由;
(2)若AB=1,求点D到AC的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图回答以下问题
(1) 若
 ,可以得到哪两条线段平行?直接填空: ∥ (不用说明理由)
,可以得到哪两条线段平行?直接填空: ∥ (不用说明理由)(2) 在(1)的结论下,如果
 ,又能得到哪两条线段平行,请说明理由.
,又能得到哪两条线段平行,请说明理由.(3) 在(2)的结论下,如果
 于
于 ,
, 30°,求
30°,求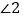 的度数.
的度数.
-
科目: 来源: 题型:
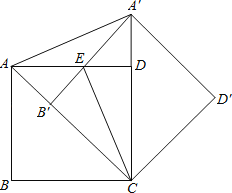
查看答案和解析>>【题目】如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.
求证:(1)△ADA′≌△CDE;
(2)直线CE是线段AA′的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师在黑板上写了一道题目,计算:
 .小宇做得最快,立刻拿给李老师看,李老师看完摇了摇头,让小宇回去认真检查.请你仔细阅读小宇的计算过程,帮助小宇改正错误.
.小宇做得最快,立刻拿给李老师看,李老师看完摇了摇头,让小宇回去认真检查.请你仔细阅读小宇的计算过程,帮助小宇改正错误.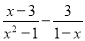 =
= ----(A)
----(A)=
 ----(B)
----(B)=
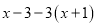 ---(C)
---(C)=
 ---(D)
---(D)(1) 上述计算过程中,哪一步开始出现错误? ;(用字母表示)
(2) 从(B)到(C)是否正确? ;若不正确,错误的原因是 ;
(3) 请你写出此题完整正确的解答过程.
相关试题

