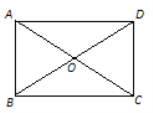
【题目】如图,在矩形ABCD中,对角线AC、BD相交于O,且AC=2AB.
(1)你能说明△AOB是等边三角形吗?请写出理由;
(2)若AB=1,求点D到AC的距离.
参考答案:
【答案】(1)△OAB是等边三角形(2)DE=![]()
【解析】试题分析:(1)根据矩形的对角线互相平分且相等可得OA=OB,再求出AB=![]() AC,然后根据三条边都相等的三角形是等边三角形解答;
AC,然后根据三条边都相等的三角形是等边三角形解答;
(2)在Rt△ABC中,根据勾股定理求出BC的长, 作DE⊥AC于E,利用三角形的面积法即可求得DE长.
试题解析:(1)△OAB是等边三角形, 理由如下:
在矩形ABCD中,OA=OC,OB=OD, AC=BD,
∴ OA=![]() AC,OB=
AC,OB=![]() BD.
BD.
又∵ AB=![]() AC,
AC,
∴ OA=OB=AB,
即△OAB是等边三角形;
(2)在Rt△ABC中,AB=1,AC=2,
根据勾股定理,得BC=![]() ,
,
作DE⊥AC于E,
∴ DE·AC=AD·DC,
∴ DE=![]()

-
科目: 来源: 题型:
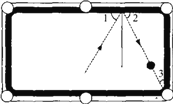
查看答案和解析>>【题目】(1)如图所示,选择适当的方向击打白球,可以使白球 反弹后将黑球撞入袋中,此时∠1=∠2,并且∠2 +∠3=90°。如果∠3=30°,那么∠1应等于多少度,才能保证黑球直接入袋?
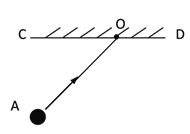
(2)如图,打台球时,小球由A点出发撞击到台球桌边CD的点O处,请用尺规作图的方法作出小球反弹后的运动方向(不写作法,但要保留作图痕迹)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:a3a=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A1(-1,1),A2(2,4),A3(-3,9),A4(4,16),…,用你发现的规律确定点A9的坐标为____.
-
科目: 来源: 题型:
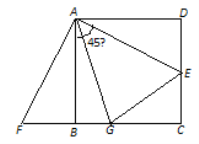
查看答案和解析>>【题目】如图,已知正方形ABCD的边长是2,E是DC上一点,△ADE经顺时针旋转后与△ABF重合.
(1)指出旋转的中心和旋转的角度;
(2)如果连结EF,那么△AEF是怎样的三角形?请说明理由.
(3)已知点G在BC上,且∠GAE=45°.
① 试说明GE=DE+BG.
② 若E是DC的中点,求BG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图回答以下问题
(1) 若
 ,可以得到哪两条线段平行?直接填空: ∥ (不用说明理由)
,可以得到哪两条线段平行?直接填空: ∥ (不用说明理由)(2) 在(1)的结论下,如果
 ,又能得到哪两条线段平行,请说明理由.
,又能得到哪两条线段平行,请说明理由.(3) 在(2)的结论下,如果
 于
于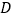 ,
, 30°,求
30°,求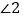 的度数.
的度数.
-
科目: 来源: 题型:
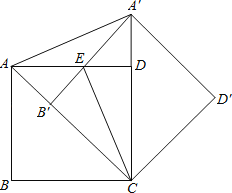
查看答案和解析>>【题目】如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.
求证:(1)△ADA′≌△CDE;
(2)直线CE是线段AA′的垂直平分线.
相关试题

