【题目】如图,直线y=x+3与两坐标轴交于A,B两点,抛物线y=﹣x2+bx+c过A、B两点,且交x轴的正半轴于点C.
(1)直接写出A、B两点的坐标;
(2)求抛物线的解析式和顶点D的坐标;
(3)在抛物线上是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.

参考答案:
【答案】(1)B(0,3),A(﹣3,0);(2)抛物线解析式为:y=﹣x2﹣2x+3;顶点D坐标为(﹣1,4);(3)存在,符合条件的点P的坐标为(﹣1,4)或(2,﹣5).
【解析】试题分析:(1)分别令x=0和y=0代入y=x+3中可得结论;
(2)利用待定系数法求二次函数的解析式,根据配方法可得顶点D的坐标;
(3)分两种情况:设点P的坐标为(t,﹣t2﹣2t+3).根据两点距离公式可得:AB2=32+32=18,AP2=(t+3)2+(﹣t2﹣2t+3)2,BP2=t2+(﹣t2﹣2t)2.
①如图1,如果点B为直角顶点,那么AB2+BP2=AP2;
②如图2,如果点A为直角顶点,那么AP2+AB2=BP2,列方程可得结论.
试题解析:解:(1)当x=0时,y=3,∴B(0,3),当y=0时,x+3=0,x=﹣3,∴A(﹣3,0);
(2)把A(﹣3,0),B(0,3)分别代入y=﹣x2+bx+c得:
![]() ,解得:
,解得: ![]() ,∴抛物线解析式为:y=﹣x2﹣2x+3;
,∴抛物线解析式为:y=﹣x2﹣2x+3;
顶点D坐标为(﹣1,4)
(3)存在.
设点P的坐标为(t,﹣t2﹣2t+3).
∵A(﹣3,0),B(0,3),∴AB2=32+32=18,AP2=(t+3)2+(﹣t2﹣2t+3)2,BP2=t2+(﹣t2﹣2t)2.
当△PAB是以AB为直角边的直角三角形时,可分两种情况:
①如图1,如果点B为直角顶点,那么AB2+BP2=AP2
(事实这里的点P与点D 重合)
即18+t2+(﹣t2﹣2t)2=(t+3)2+(﹣t2﹣2t+3)2,整理得t2+t=0,解得t1=﹣1,t2=0(不合题意舍去),则点P的坐标为(﹣1,4);
②如图2,如果点A为直角顶点,那么AP2+AB2=BP2,即18+(t+3)2+(﹣t2﹣2t+3)2=t2+(﹣t2﹣2t)2,整理得t2+t﹣6=0,解得t1=2,t2=﹣3(不合题意舍去),则点P的坐标为(2,﹣5);
综上所述:所有符合条件的点P的坐标为(﹣1,4)或(2,﹣5).
另解:如图3,作DE⊥y轴于点E,发现∠ABO=∠DBE=45°
可知顶点D满足△DAB是直角三角形,这时点P的坐标为(﹣1,4);
作PA⊥AB交抛物线于点P,作PF⊥x轴于点F,发现∠PAF=∠APF=45°,由PF=AF求出另一点P为(2,﹣5).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列三行数:
0,3,8,15,24,…①
2,5,10,17,26,…②
0,6,16,30,48,…③
(1)第①行数按什么规律排的,请写出来?
(2)第②、③行数与第①行数分别对比有什么关系?
(3)取每行的第
 个数,求这三个数的和.
个数,求这三个数的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,一个数在数轴上所对应的点与原点之间的距离就是这个数的绝对值。那么任意两个数与它们在数轴上所对应的点之间的距离又有什么关系呢?
(1)如图所示,-3,-1,2,4在数轴上分别对应点
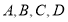 。
。
则①点
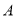 与原点之间的距离为_______________;②
与原点之间的距离为_______________;②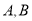 两点之间的距离为_____________;
两点之间的距离为_____________;③
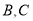 两点之间的距离为______________;④
两点之间的距离为______________;④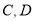 两点之间的距离为_______________。
两点之间的距离为_______________。你的结论:如果两个数
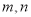 在数轴上分别对应点
在数轴上分别对应点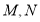 ,那么
,那么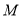 与
与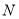 两点之间的距离表示为______________________。(用含
两点之间的距离表示为______________________。(用含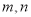 的式子表示)
的式子表示)(2)利用(1)的结论解决下列问题:
已知数轴上点
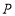 对应
对应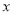 ,点
,点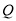 对应3,且
对应3,且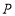 与
与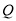 之间的距离是8,求
之间的距离是8,求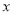 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,假分数可以化为整数与真分数的和的形式,例如
 =1+
=1+ .在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像
.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像 ……这样的分式是假分式;像
……这样的分式是假分式;像 ,……这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式,例如:
,……这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式,例如:

(1)分式
 是 分式(填“真”或“假”);
是 分式(填“真”或“假”);(2)将分式
 化成整式与真分式的和的形式;
化成整式与真分式的和的形式;(3)如果分式
 的值为整数,求x的整数值.
的值为整数,求x的整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意及解答过程填空:
如图所示,AB=10cm,D为AC的中点,DC=2cm,BE=
 BC,求CE的长。
BC,求CE的长。
解:因为D为AC的中点,DC=2cm.
所以AC="_______DC=_______" cm.
由图可知:BC="______" -AC
="10" cm-____cm
=_______cm.
所以BE=
 BC=______cm.
BC=______cm.所以CE=BC-BE=_____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近几年,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,我们国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:

(1)根据上图填写下表:
平均数
中位数
众数
方差
甲班
8.5
乙班
8.5
10
1.6
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度对甲乙两班进行分析.
相关试题

