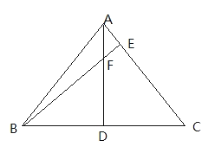
【题目】如图,已知在△ABC中,AD⊥BC于点D,BE⊥AC于点E,且DF=DC。
(1)求证:BD=AD;
(2)若AF=1,DC=3,求BF的长.
参考答案:
【答案】(1)证明见解析;(2)BF=5
【解析】
(1)、根据AD⊥BC和AC⊥BE得出∠EBC+∠C=90° ,∠CAD+∠C=90°,从而得出∠CAD=∠EBC,结合DF=DC得出△ACD和△BFD全等,从而得出答案;(2)、根据全等得出AF=1,DC=3,DF=DC,BD=AD=4,最后根据Rt△ADC的勾股定理求出AC的长度,即BF的长度.
(1)证明:∵ AD⊥BC,
∴ △ACD和△BFD是直角三角形 (两边相互垂直的三角形是直角三角形),∵ AC⊥BE,
∴ ∠BEC=90°,∴ ∠EBC+∠C=90°,∵ △ACD是直角三角形,
∴ ∠CAD+∠C=90° (直角三角形的两个锐角互余),
∵ ∠EBC+∠C=90° ,∠CAD+∠C=90°,∴ ∠CAD=∠EBC,∴ △ACD≌△BFD(AAS),
∴ BD=AD(全等三角形的对应边相等),
(2)、由(1)得△ACD≌△BFD, ∴BD=AD,AD=AC(全等三角形的对应边相等),
∵AF=1,DC=3,DF=DC, ∴BD=AD=4,又∵AD⊥BC,
∴AD2+DC2=AC2(勾股定理), ∴BF=AC=5.
-
科目: 来源: 题型:
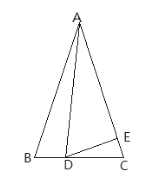
查看答案和解析>>【题目】如图,已知在△ABC中,∠ABC=65°,AB=AC,∠BAD=20°,AD=AE,求∠EDC的度数.
-
科目: 来源: 题型:
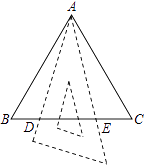
查看答案和解析>>【题目】如图,△ABC是边长为a的等边三角形,将三角板的30°角的顶点与A重合,三角板30°角的两边与BC交于D、E两点,则DE长度的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC与点O在10×10的网格中的位置如图所示

(1)画出△ABC绕点O逆时针旋转90°后的图形;
(2)画出△ABC绕点O逆时针旋转180°后的图形;
(3)若⊙M能盖住△ABC,则⊙M的半径最小值为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+
∠AOB=60°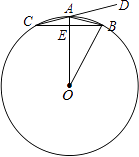
(1)求∠AOB的度数;
(2)若AE=1,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】飞机着陆后滑行的距离S(单位:m)关于滑行时间t(单位:s)的函数解析式是:S=60t﹣1.5t2
(1)直接指出飞机着陆时的速度;
(2)直接指出t的取值范围;
(3)画出函数S的图象并指出飞机着陆后滑行多远才能停下来?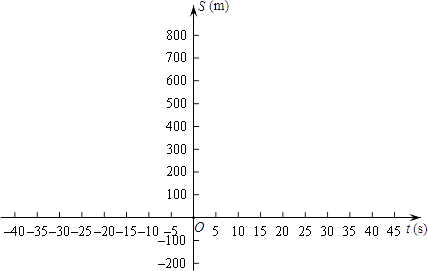
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6cm的等边三角形,点D从B点出发沿B→A方向在线段BA上以a cm/s速度运动,与此同时,点E从线段BC的某个端点出发,以b cm/s速度在线段BC上运动,当D到达A点后,D、E运动停止,运动时间为t(秒)
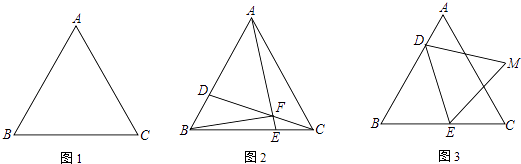
(1)如图1,若a=b=1,点E从C出发沿C→B方向运动,连AE、CD,AE、CD交于F,连BF.当0<t<6时:
①求∠AFC的度数;
②求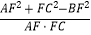 的值;
的值;
(2)如图2,若a=1,b=2,点E从B点出发沿B→C方向运动,E点到达C点后再沿C→B方向运动.当t≥3时,连DE,以DE为边作等边△DEM,使M、B在DE两侧,求M点所经历的路径长.
相关试题

