【题目】飞机着陆后滑行的距离S(单位:m)关于滑行时间t(单位:s)的函数解析式是:S=60t﹣1.5t2
(1)直接指出飞机着陆时的速度;
(2)直接指出t的取值范围;
(3)画出函数S的图象并指出飞机着陆后滑行多远才能停下来? 
参考答案:
【答案】
(1)
解:飞机着陆时的速度V=60;
(2)
解:当S取得最大值时,飞机停下来,
则S=60t﹣1.5t2=﹣1.5(x﹣20)2+600,
此时t=20
因此t的取值范围是0≤t≤20;
(3)
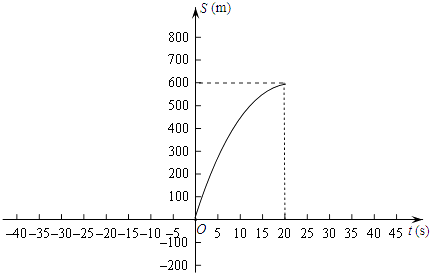
解:如图,
S=60t﹣1.5t2=﹣1.5(x﹣20)2+600.
飞机着陆后滑行600米才能停下来.
【解析】(1)直接由函数解析式得出答案即可;(2)由于飞机着陆,不会倒着跑,所以当S取得最大值时,t也取得最大值,求得t的取值范围即可;(3)利用配方法求得函数的最值,也就是飞机着陆后滑行的最远距离.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC与点O在10×10的网格中的位置如图所示

(1)画出△ABC绕点O逆时针旋转90°后的图形;
(2)画出△ABC绕点O逆时针旋转180°后的图形;
(3)若⊙M能盖住△ABC,则⊙M的半径最小值为多少? -
科目: 来源: 题型:
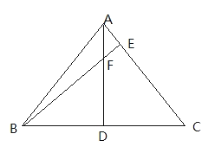
查看答案和解析>>【题目】如图,已知在△ABC中,AD⊥BC于点D,BE⊥AC于点E,且DF=DC。
(1)求证:BD=AD;
(2)若AF=1,DC=3,求BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+
∠AOB=60°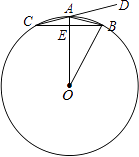
(1)求∠AOB的度数;
(2)若AE=1,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6cm的等边三角形,点D从B点出发沿B→A方向在线段BA上以a cm/s速度运动,与此同时,点E从线段BC的某个端点出发,以b cm/s速度在线段BC上运动,当D到达A点后,D、E运动停止,运动时间为t(秒)
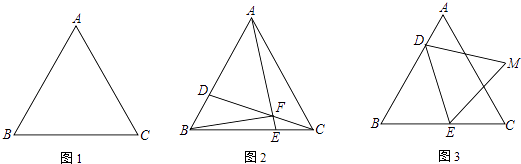
(1)如图1,若a=b=1,点E从C出发沿C→B方向运动,连AE、CD,AE、CD交于F,连BF.当0<t<6时:
①求∠AFC的度数;
②求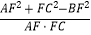 的值;
的值;
(2)如图2,若a=1,b=2,点E从B点出发沿B→C方向运动,E点到达C点后再沿C→B方向运动.当t≥3时,连DE,以DE为边作等边△DEM,使M、B在DE两侧,求M点所经历的路径长. -
科目: 来源: 题型:
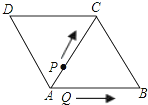
查看答案和解析>>【题目】如图,△ABC和△ACD都是边长为2厘米的等边三角形,两个动点P,Q同时从A点出发,点P以0.5厘米/秒的速度沿A→C→B的方向运动,点Q以1厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动。设P、Q运动的时间为t秒
(1)当t=2时,PQ=___;
(2)求点P、Q从出发到相遇所用的时间;
(3)当t取何值时,△APQ是等边三角形;请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:我们把平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹(满足条件的所有点所组成的图形)叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
(1)已知抛物线的焦点F(0,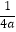 ),准线l:
),准线l: 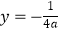 ,求抛物线的解析式;
,求抛物线的解析式;
(2)已知抛物线的解析式为:y=x2﹣n2 , 点A(0,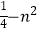 )(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
)(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
(3)若(2)中抛物线的顶点为C,抛物线与x轴的两个交点分别是D、E,过C、D、E三点作⊙M,⊙M上是否存在定点N?若存在,求出N点坐标并指出这样的定点N有几个;若不存在,请说明理由.
相关试题

