【题目】尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).

参考答案:
【答案】作图见解析.
【解析】试题分析:分别作出AD的垂直平分线及∠ABC的平分线,两条直线的交点即为P点的位置.
试题解析:(1)①分别以A、D为圆心,以大于![]() AD为半径画圆,两圆相交于E、F两点;
AD为半径画圆,两圆相交于E、F两点;
②连接EF,则EF即为线段AD的垂直平分线.
(2)①以B为圆心,以大于任意长为半径画圆,分别交AB、BC为G、H;
②分别以G、H为圆心,以大于![]() GH为半径画圆,两圆相交于点I,连接BI,则BI即为∠ABC的平分线.
GH为半径画圆,两圆相交于点I,连接BI,则BI即为∠ABC的平分线.
③BI与EF相交于点P,则点P即为所求点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CEF其中正确的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)如图,在四边形ABCD中,AD∥BC,点E在BC的延长线上,CE=BC,连接AE,交CD边于点F,且CF=DF.(1)求证:AD=BC;(2)连接BD、DE,若BD⊥DE,求证:四边形ABCD为菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C、P四点均在边长为1的小正方形网格格点上.
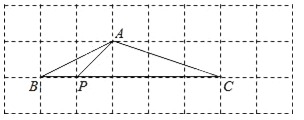
(1)判断△PBA与△ABC是否相似,并说明理由;
(2)求∠BAC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体纸箱的长、宽、高分别为50cm、30cm、60cm,一只蚂蚁从点A处沿着纸箱的表面爬到点B处.蚂蚁爬行的最短路程为_______cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,直线
,直线 分别与
分别与 、
、 交于点
交于点 、点
、点 .
.(1)如图1,当点
 在线段
在线段 上,若
上,若 ,
, ,则
,则 __________°;
__________°;
(2)如图2,当点
 在线段
在线段 的延长线上,
的延长线上, 与
与 交于点
交于点 ,则
,则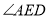 、
、 、
、 之间满足怎样的关系,请证明你的结论;
之间满足怎样的关系,请证明你的结论;
(3)如图3,在(2)的条件下,
 平分
平分 ,交
,交 于点
于点 ,射线
,射线 将
将 分成
分成 ,且与
,且与 交于点
交于点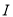 ,若
,若 ,
, ,求
,求 的度数.
的度数.
相关试题

