【题目】如图,A、B、C、P四点均在边长为1的小正方形网格格点上.
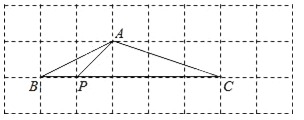
(1)判断△PBA与△ABC是否相似,并说明理由;
(2)求∠BAC的度数.
参考答案:
【答案】(1)相似;(2)135°.
【解析】试题分析:(1)△PBA与△ABC相似,利用勾股定理计算出AB的长,利用两边对应成比例且一个夹角对应相等的两个三角形相似可证明结论成立;
(2)由(1)可知:∠BAC=∠BPA,因为∠BPA易求,问题得解.
试题解析:解:(1)△PBA与△ABC相似.理由如下:
∵AB=![]() ,BC=5,BP=1,∴
,BC=5,BP=1,∴![]() .∵∠PBA=∠ABC,∴△PBA∽△ABC;
.∵∠PBA=∠ABC,∴△PBA∽△ABC;
(2)∵△PBA∽△ABC,∴∠BAC=∠BPA.∵∠BPA=90°+45°=135°,∴∠BAC=135°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且BC=8cm,CA=6cm,则点O到边AB的距离为( )
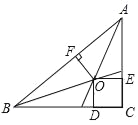
A. 2cm B. 3cm C. 4cm D. 5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CEF其中正确的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)如图,在四边形ABCD中,AD∥BC,点E在BC的延长线上,CE=BC,连接AE,交CD边于点F,且CF=DF.(1)求证:AD=BC;(2)连接BD、DE,若BD⊥DE,求证:四边形ABCD为菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体纸箱的长、宽、高分别为50cm、30cm、60cm,一只蚂蚁从点A处沿着纸箱的表面爬到点B处.蚂蚁爬行的最短路程为_______cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
相关试题

