【题目】课本上有这样一道例题:
例 已知等腰三角形底边长为a, 底边上的高的长为h,求作这个等腰三角.

作法:(1)作线段AB=a,
(2)作线段AB的垂直平分线MN,与AB相交于点D,
(3)在MN上取一点C,使DC=h,
(4)连接AC,BC,则△ABC就是所求作的等腰三角形.
请你思考只要CD垂直平分AB,那么△ABC就是等腰三角形的依据是_____.
参考答案:
【答案】线段垂直平分线上的点与这条线段两端点距离相等,等腰三角形定义.
【解析】
按照作法作图,根据线段垂直平分线的性质即可判断AC=BC,再由等腰三角形的定义即可得出结论.
作图如下:
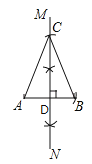
只要CD垂直平分AB,那么△ABC就是等腰三角形的依据是线段垂直平分线上的点与这条线段两端点距离相等,等腰三角形定义.
故答案为:线段垂直平分线上的点与这条线段两端点距离相等,等腰三角形定义.
-
科目: 来源: 题型:
查看答案和解析>>【题目】读句画图:如图,直线CD与直线AB相交于C,
根据下列语句画图:

(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AC的长为( )
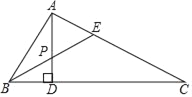
A. 2 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
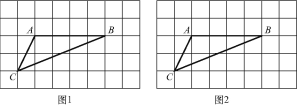
查看答案和解析>>【题目】如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且以A,B,C,D为顶点的四边形是轴对称图形;
(2)在图2中画△ABE(点E在小正方形的顶点上),使△ABE的周长等于△ABC的周长,且以A,B,C,E为顶点的四边形是中心对称图形,并直接写出该四边形的面积.
-
科目: 来源: 题型:
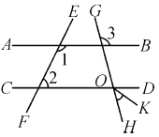
查看答案和解析>>【题目】已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.
(1)直线AB与CD有怎样的位置关系?说明理由;
(2)∠KOH的度数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长均为
 个单位的正方形网格图中,建立了直角坐标系
个单位的正方形网格图中,建立了直角坐标系 ,按要求解答下列问题:
,按要求解答下列问题:
(1)写出
 三个顶点的坐标;
三个顶点的坐标;(2)画出
 向右平移
向右平移 个单位后的图形
个单位后的图形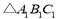 ;
;(3)求
 在平移过程中扫过的面积.
在平移过程中扫过的面积.
相关试题

