【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
参考答案:
【答案】见解析
【解析】
(1)连接BE,根据线段垂直平分线的性质可得AE=BE,利用等边对等角的性质可得∠ABE=∠A;结合三角形外角的性质可得∠BEC的度数,再在Rt△BCE中结合含30°角的直角三角形的性质,即可证明第(1)问的结论;
(2)根据直角三角形斜边中线的性质可得BD=CD,再利用直角三角形锐角互余的性质可得到∠ABC=60°,至此不难判断△BCD的形状
(1)证明:连结BE,如图.
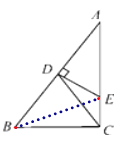
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABC-∠ABE=30°,
在Rt△BCE中,BE=2CE,
∴AE=2CE.
(2)解:△BCD是等边三角形.
理由如下:
∵DE垂直平分AB,
∴D为AB的中点.
∵∠ACB=90°,
∴CD=BD.
又∵∠ABC=60°,
∴△BCD是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
社团类别
人数
占总人数比例
球类
60
m
舞蹈
30
0.25
健美操
n
0.15
武术
12
0.1

(1)求样本容量及表格中m、n的值;
(2)请补全统计图;
(3)被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3000名学生,请估计该校最喜欢足球的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=60°,AB的垂直平分线分别交AB,AC于点D和点E.若CE=2,则AB的长是_____.
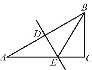
-
科目: 来源: 题型:
查看答案和解析>>【题目】读句画图:如图,直线CD与直线AB相交于C,
根据下列语句画图:

(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AC的长为( )
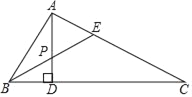
A. 2 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】课本上有这样一道例题:
例 已知等腰三角形底边长为a, 底边上的高的长为h,求作这个等腰三角.

作法:(1)作线段AB=a,
(2)作线段AB的垂直平分线MN,与AB相交于点D,
(3)在MN上取一点C,使DC=h,
(4)连接AC,BC,则△ABC就是所求作的等腰三角形.
请你思考只要CD垂直平分AB,那么△ABC就是等腰三角形的依据是_____.
-
科目: 来源: 题型:
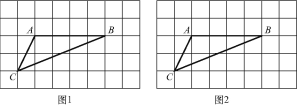
查看答案和解析>>【题目】如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且以A,B,C,D为顶点的四边形是轴对称图形;
(2)在图2中画△ABE(点E在小正方形的顶点上),使△ABE的周长等于△ABC的周长,且以A,B,C,E为顶点的四边形是中心对称图形,并直接写出该四边形的面积.
相关试题

