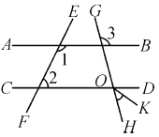
【题目】已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.
(1)直线AB与CD有怎样的位置关系?说明理由;
(2)∠KOH的度数是多少?
参考答案:
【答案】(1)AB∥CD,理由见解析;(2)40°.
【解析】
(1)根据同旁内角互补两直线平行可判定AB∥CD;
(2)由已知条件结合平行线的性质可求得∠GOD,再结合邻补角和角平分线的定义可求得∠KOH.
解:(1)AB∥CD,
理由如下:
∵∠1+∠2=180°,
∴AB∥CD;
(2)∵AB∥CD,∠3=100°,
∴∠GOD=∠3=100°,
∵∠GOD+∠DOH=180°,
∴∠DOH=80°,
∵OK平分∠DOH,
∴∠KOH =![]() ∠DOH=40°.
∠DOH=40°.
故答案为:(1)AB∥CD,理由见解析;(2)40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AC的长为( )
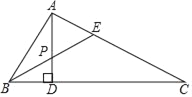
A. 2 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】课本上有这样一道例题:
例 已知等腰三角形底边长为a, 底边上的高的长为h,求作这个等腰三角.

作法:(1)作线段AB=a,
(2)作线段AB的垂直平分线MN,与AB相交于点D,
(3)在MN上取一点C,使DC=h,
(4)连接AC,BC,则△ABC就是所求作的等腰三角形.
请你思考只要CD垂直平分AB,那么△ABC就是等腰三角形的依据是_____.
-
科目: 来源: 题型:
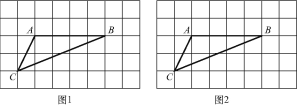
查看答案和解析>>【题目】如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且以A,B,C,D为顶点的四边形是轴对称图形;
(2)在图2中画△ABE(点E在小正方形的顶点上),使△ABE的周长等于△ABC的周长,且以A,B,C,E为顶点的四边形是中心对称图形,并直接写出该四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长均为
 个单位的正方形网格图中,建立了直角坐标系
个单位的正方形网格图中,建立了直角坐标系 ,按要求解答下列问题:
,按要求解答下列问题:
(1)写出
 三个顶点的坐标;
三个顶点的坐标;(2)画出
 向右平移
向右平移 个单位后的图形
个单位后的图形 ;
;(3)求
 在平移过程中扫过的面积.
在平移过程中扫过的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60
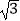 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: 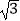 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°=
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°= 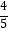 ,cos
,cos 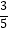 =
= 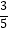 ,tan53°=
,tan53°=  ,
, 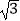 ≈1.732,结果精确到0.1米)
≈1.732,结果精确到0.1米)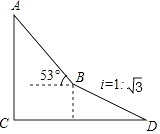
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:
材料一:大家知道
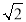 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此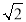 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用 来表示
来表示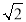 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为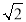 的整数部分是1,将这个数减去其整数部分,差就是小数部分.由此我们得到一个真命题:
的整数部分是1,将这个数减去其整数部分,差就是小数部分.由此我们得到一个真命题:如果
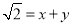 ,其中
,其中 是整数,且
是整数,且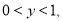 那么
那么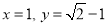 .
.材料二:已知
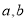 是有理数,并且满足等式
是有理数,并且满足等式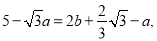 求
求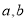 的值.
的值.解:

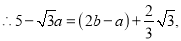
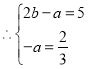 ,解得
,解得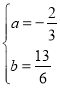
请解答:
(1)如果
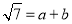 ,其中
,其中 是整数,且
是整数,且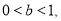 那么
那么 _______,
_______,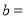 ______.
______.(2)如果
 的小数部分为
的小数部分为 ,
,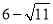 的整数部分为
的整数部分为 ,求
,求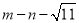 的值;
的值;(3)已知
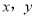 是有理数,并且满足等式
是有理数,并且满足等式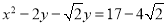 ,求
,求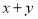 的值.
的值.
相关试题

