【题目】如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.

参考答案:
【答案】(1)证明见解析;(2)4.
【解析】
试题(1)、首先证明△ABC≌△DFE可得∠ACE=∠DEF,进而可得AC∥DE;(2)、根据△ABC≌△DFE可得BC=EF,利用等式的性质可得EB=CF,再由BF=13,EC=5进而可得EB的长,然后可得答案.
试题解析:(1)、在△ABC和△DFE中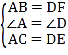 , ∴△ABC≌△DFE(SAS), ∴∠ACE=∠DEF, ∴AC∥DE;
, ∴△ABC≌△DFE(SAS), ∴∠ACE=∠DEF, ∴AC∥DE;
(2)、∵△ABC≌△DFE, ∴BC=EF, ∴CB﹣EC=EF﹣EC, ∴EB=CF, ∵BF=13,EC=5,
∴EB=4, ∴CB=4+5=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场二楼摆出一台游戏装置如图所示,小球从最上方入口处投入,每次遇到黑色障碍物,等可能地向左或向右边落下.

(1)若乐乐投入一个小球,则小球落入B区域的概率为 .
(2)若乐乐先后投两个小球,求两个小球同时落在A区域的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,ABCD 中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F.
(1)求证:四边形EBFD是平行四边形;
(2)小明在完成(1)的证明后继续进行了探索.连接AF、CE,分别交BE、FD于点G、H,得到四边形EGFH.此时,他猜想四边形EGFH是平行四边形,请在框图(图2)中补全他的证明思路.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC是正方形,过点B(2,2)的直线l与y轴交于点D,且OD=AD,直线l上的点E在第三象限,且到x轴的距离为
 .
. 
(1)求直线l的表达式;
(2)若反比例函数y= 的图象经过点E,求k的值.
的图象经过点E,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF.
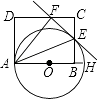
(1)求证:直线EF是⊙O的切线.
(2)若CD=10,EB=5,求⊙O的直径. -
科目: 来源: 题型:
查看答案和解析>>【题目】学生在操场上利用三角函数测量旗杆AB的高,直线l为水平地面,两个同学把30°的三角板和量角器按如图所示的方式垂直放在地面上,量角器的零刻度线与地面重合,此时旗杆顶部B的影子恰好落在三角形板的顶点D处和量角器37°的刻度C处,已知三角形板的边DE=60厘米,量角器的半径r=25厘米,量角器的圆心O到A的距离为5米.

(1)则∠AOC=°(直接写出答案)
(2)求旗杆AB的高度(精确到0.1米,参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ≈1.73)
≈1.73) -
科目: 来源: 题型:
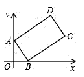
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2,BC=4,点A、B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是 .
相关试题

