【题目】学生在操场上利用三角函数测量旗杆AB的高,直线l为水平地面,两个同学把30°的三角板和量角器按如图所示的方式垂直放在地面上,量角器的零刻度线与地面重合,此时旗杆顶部B的影子恰好落在三角形板的顶点D处和量角器37°的刻度C处,已知三角形板的边DE=60厘米,量角器的半径r=25厘米,量角器的圆心O到A的距离为5米. 
(1)则∠AOC=°(直接写出答案)
(2)求旗杆AB的高度(精确到0.1米,参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ![]() ≈1.73)
≈1.73)
参考答案:
【答案】
(1)37
(2)解:过C作CP⊥直线l,过C作CM⊥AB于M,过D作N⊥AB于N,
在Rt△OCP中,CP=OCsin37°≈0.25×0.6=0.15米,OP=OCcos37°≈0.25×0.8=0.2米;
∵CM⊥AB,DN⊥AB,
∴CM∥DN,
∴△BND∽△BMC,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AB≈5.6米,
答:旗杆AB的高度为5.6米.
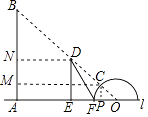
【解析】解:(1)∠AOC=37°,
所以答案是:37;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC是正方形,过点B(2,2)的直线l与y轴交于点D,且OD=AD,直线l上的点E在第三象限,且到x轴的距离为
 .
. 
(1)求直线l的表达式;
(2)若反比例函数y= 的图象经过点E,求k的值.
的图象经过点E,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF.
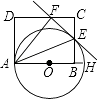
(1)求证:直线EF是⊙O的切线.
(2)若CD=10,EB=5,求⊙O的直径. -
科目: 来源: 题型:
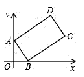
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2,BC=4,点A、B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是 .
-
科目: 来源: 题型:
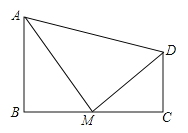
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM;
(2)M为BC的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将点A先向右平移3个单位长度,在向下平移5个单位长度,得到A’;将点B先向下平移5个单位长度,再向右平移4个单位长度,得到B’,则A’与B’相距( )

A. 4个单位长度 B. 5个单位长度 C. 6个单位长度 D. 7个单位长度
相关试题

