【题目】某商场二楼摆出一台游戏装置如图所示，小球从最上方入口处投入，每次遇到黑色障碍物，等可能地向左或向右边落下．

（1）若乐乐投入一个小球，则小球落入B区域的概率为 ．
（2）若乐乐先后投两个小球，求两个小球同时落在A区域的概率．

参考答案：

【答案】
（1）
（2）解：先后共投2个小球，可能会出现的结果列树状图如下：

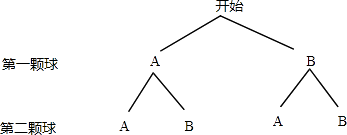
由树状图可知，共有4种等可能情况，其中2个小球均落在A区只有1种情况，

则2个小球均落在A区的概率为


【解析】解：（1）∵乐乐投入一个小球，

∴小球落入B区域的概率为 ；

所以答案是： ；

【考点精析】认真审题，首先需要了解列表法与树状图法(当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率)，还要掌握概率公式(一般地，如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，事件A包含其中的m中结果，那么事件A发生的概率为P（A）=m/n)的相关知识才是答题的关键．

关闭