【题目】如图1,ABCD 中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F.
(1)求证:四边形EBFD是平行四边形;
(2)小明在完成(1)的证明后继续进行了探索.连接AF、CE,分别交BE、FD于点G、H,得到四边形EGFH.此时,他猜想四边形EGFH是平行四边形,请在框图(图2)中补全他的证明思路.

参考答案:
【答案】(1)四边形EBFD是平行四边形.
(2)GF∥EH,AE∥CF;
【解析】
试题分析:(1)由平行四边形的性质得出AD∥BC,∠ABC=∠ADC.AD=BC,由角平分线得出∠ABE=∠EBC=∠ADF=∠CDF.证出EB∥DF,即可得出结论;
(2)由平行四边形的性质得出BE∥DF,DE=BF,得出AE=CF,证出四边形AFCE是平行四边形,得出GF∥EH,即可证出四边形EGFH是平行四边形.
试题解析:(1)证明:在ABCD中,AD∥BC,∠ABC=∠ADC.AD=BC,
∵BE平分∠ABC,
∴∠ABE=∠EBC=![]() ∠ABC.
∠ABC.
∵DF平分∠ADC,
∴∠ADF=∠CDF=![]() ∠ADC.
∠ADC.
∵∠ABC=∠ADC.
∴∠ABE=∠EBC=∠ADF=∠CDF.
∵AD∥BC,
∴∠AEB=∠EBC.
∴∠AEB=∠ADF.
∴EB∥DF.
∵ED∥BF,
∴四边形EBFD是平行四边形.
(2)补全思路:GF∥EH,AE∥CF;理由如下:
∵四边形EBFD是平行四边形;
∴BE∥DF,DE=BF,
∴AE=CF,
又∵AE∥CF,
∴四边形AFCE是平行四边形,
∴GF∥EH,
∴四边形EGFH是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在墙壁上固定一根横放的木条,则至少需要( )枚钉子.
A. l B. 2 C. 3 D. 随便多少枚
-
科目: 来源: 题型:
查看答案和解析>>【题目】A种饮料比B种饮料单价少1元,小峰买了3瓶A种饮料和4瓶B种饮料,一共花了18元.如果设B种饮料单价为x元/瓶,那么下面所列方程正确的是 ( )
A.3x+4(x-1)=18 B.3(x+1)+4x=18
C.3x+4(x+1)=18 D.3(x-1)+4x=18
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:3a3b﹣3ab3=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉嘉将长为
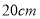 ,宽为
,宽为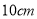 的长方形白纸按图所示的方法粘在一起,黏合部分(图中阴影部分)的宽为
的长方形白纸按图所示的方法粘在一起,黏合部分(图中阴影部分)的宽为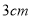 .
.(1)求
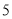 张白纸粘在一起后的长度;
张白纸粘在一起后的长度;(2)设
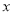 张白纸粘在一起后总长为
张白纸粘在一起后总长为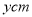 .写出
.写出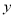 与
与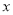 之间的函数关系式;
之间的函数关系式;(3)求当
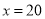 时
时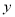 的值,并说明它在题目中的实际意义.
的值,并说明它在题目中的实际意义.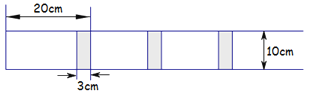
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读可以增进人们的知识也能陶冶人们的情操.我们要多阅读,多阅读有营养的书.因此我校对学生的课外阅读时间进行了抽样调查,将收集的数据分成
 、
、 、
、 、
、 、
、 五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).
五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).请结合以上信息解答下列问题
(1)求
 ,
,  ,
,  的值;
的值;(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在
 以下(不含
以下(不含 )的学生所占百分比.
)的学生所占百分比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用
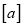 表示不大于
表示不大于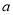 的最大整数,例如:
的最大整数,例如: 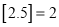 ,
, 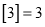 ,
, 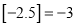 ;用
;用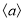 表示大于
表示大于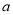 的最小整数,例如:
的最小整数,例如: 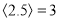 ,
, 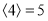 ,
, 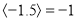 .解决下列问题:
.解决下列问题:(1)
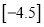 = ,,
= ,, 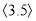 = ;
= ;(2)若
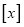 =2,则
=2,则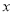 的取值范围是 ;若
的取值范围是 ;若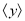 =-1,则
=-1,则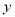 的取值范围是 ;
的取值范围是 ;(3)已知
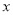 ,
, 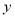 满足方程组
满足方程组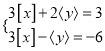 ,求
,求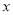 ,
, 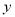 的取值范围.
的取值范围.
相关试题

