【题目】如图,在平面直角坐标系内,点![]() 为坐标原点,
为坐标原点,![]() 的顶点
的顶点![]() 在
在![]() 轴正半轴,顶点
轴正半轴,顶点![]() 、
、![]() 分别在
分别在![]() 轴负半轴和正半轴上,
轴负半轴和正半轴上,![]() ,
,![]() ,
,![]()
(1)求![]() 的长.
的长.
(2)动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 向终点
向终点![]() 运动,点
运动,点![]() 运动的时间为
运动的时间为![]() ,以
,以![]() 为斜边在
为斜边在![]() 右边上方作等腰直角三角形
右边上方作等腰直角三角形![]() ,连接
,连接![]() 、
、![]() ,设
,设![]() 的面积为
的面积为![]() (
(![]() ),求
),求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围.
的取值范围.
(3)在(2)的条件下,过点![]() 作
作![]() 的垂线交
的垂线交![]() 轴于
轴于![]() ,连接
,连接![]() ,当四边形
,当四边形![]() 的面积为
的面积为![]() ,时,求
,时,求![]() 的值及
的值及![]() 点坐标.
点坐标.
参考答案:
【答案】(1)![]() ;(2)S=2t(0≤t≤4);(3)Q(0,-2).
;(2)S=2t(0≤t≤4);(3)Q(0,-2).
【解析】
(1)根据三角形面积公式求得BC的长,然后根据等腰三角形的性质求OB的长,从而利用勾股定理求解;
(2)作PM⊥BC于N,DH⊥PC于H.利用勾股定理求出PC的长(用t表示)即可解决问题;
(3)作PN⊥y轴于N,DK⊥PN于K,DH⊥PC于H,连接AH、DH.首先证明A、P、D、C四点共圆,推出∠DAC=∠DPC=45°,∠DAO=90°,由△PNQ≌△DKP,可得DP=PQ=DC,可得四边形PQCD是正方形,根据题意列出方程即可解决问题;
解:∵![]()
∴BC=8
又∵![]() 的顶点
的顶点![]() 在
在![]() 轴正半轴,顶点
轴正半轴,顶点![]() 、
、![]() 分别在
分别在![]() 轴负半轴和正半轴上,
轴负半轴和正半轴上,![]() ,
,
∴OB=OC=![]() ,
,
∴在Rt△OAB中,![]()
(2)如图1中,作DM⊥X轴于M,PK⊥DM于K交y轴于N,DH⊥PC于H,作PE⊥x轴于E,连接AH、DH.
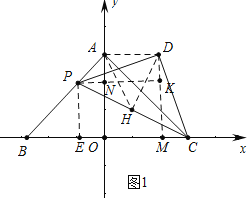
由(1)可知,OA=OB=4
∴∠BAO=∠CAO=45°,即∠BAC=90°
又∵△PCD是等腰直角三角形
∴AH=DH=HP=HC,
∴A、P、D、C四点共圆,
∴∠DAC=∠DPC=45°,
∴∠DAO=90°,
∵∠DPK+∠PDM=90°,∠PDM+∠MDC=90°,
∴∠DPK=∠MDC,
∵∠PKD=∠DMC=90°,DP=DC,
∴△PDK≌△DCM,
∴PK=DM=OA=4,
∵OA=OB,∠AOB=90°,
∴△AOB是等腰直角三角形,
∵PE⊥BC,
∴∠PEB=90°,
∴∠PBE=∠BPE=45°,
∵PB=![]() t,
t,
由题意可知,四边形PEON为矩形
∴PE=BE=t,ON=4-t,
∴CM=DK=AN=OA=ON=OA-PE=4-t,
∴AD=4-(4-t)=t,
∴S=![]()
![]() t4=2t(0≤t≤4).
t4=2t(0≤t≤4).
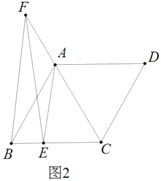
(3)如图2中,
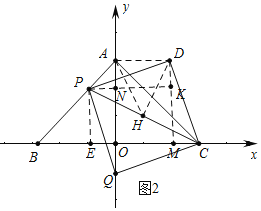
由(2)可知:PE=BE=t,ON=4-t,CE=8-t,
在Rt△PCE中,PC2=t2+(8-t)2=2t2-16t+64,
∵△PDC是等腰直角三角形,DH⊥PC,
∴PH=CH=DH,
∴S△PDC=![]() =
=![]() (0≤t≤4).
(0≤t≤4).
易知AN=PN=DK,∠QPN=∠PDK,∠PNQ=∠PKD=90°,
∴△PNQ≌△DKP,
∴DP=PQ=DC,∵PQ∥DC,
∴四边形PQCD是平行四边形,
∵∠DPQ=90°,
∴四边形PQCD是矩形,
∵PD=PQ,
∴四边形PQCD是正方形,
由题意:2(![]() )=
)=![]() ,
,
2(![]() )=10t
)=10t
整理得t2-8t+32=0,
解得:t=2或16(舍弃),
∴t=2时,四边形PDCQ的面积为20,
此时PC=2![]() ,PQ=2
,PQ=2![]() ,PN=2,ON=2,NQ=
,PN=2,ON=2,NQ=![]() =4,
=4,
∴OQ=QN-ON=2,
∴Q(0,-2).
-
科目: 来源: 题型:
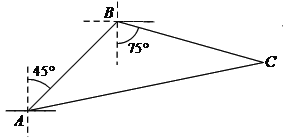
查看答案和解析>>【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,菱形
 中,
中,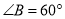 ,
,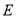 、
、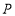 分别是边
分别是边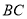 和
和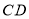 上的点,且
上的点,且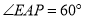 .
.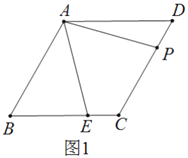
(1)求证:
(2)如图2,
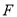 在
在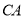 延长线上,且
延长线上,且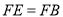 ,求证:
,求证: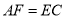
(3)如图3,在(2)的条件下,
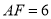 ,
,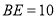 ,
,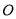 是
是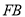 的中点,求
的中点,求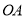 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情景:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
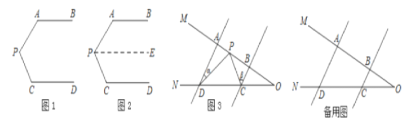
(1)天天同学看过图形后立即口答出:∠APC=110°,请你补全他的推理依据.
如图2,过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD.(___)
∴∠A+∠APE=180°.
∠C+∠CPE=180°.(___)
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.(___)
问题迁移:
(2)如图3,AD∥BC,当点P在A. B两点之间运动时,∠ADP=∠α,∠BCP=∠β,求∠CPD与∠α、∠β之间有何数量关系?请说明理由。
(3)在(2)的条件下,如果点P在A. B两点外侧运动时(点P与点A. B. O三点不重合),请你直接写出∠CPD与∠α、∠β之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中, A(-1,0),B(3,0),C(0,2),CD∥x轴,CD=AB.
(1)求点D的坐标
(2)四边形OCDB的面积

(3)在y轴上是否存在一点P,使
 =
= ,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
,若存在这样一点,求出点P的坐标,若不存在,试说明理由. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=
 ,AF=
,AF= ,求AE的长.
,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=35°,则∠HOB的度数为______.

相关试题

