搜索
【题目】如图，在平面直角坐标系中， A（-1,0），B（3,0），C（0,2），CD∥x轴，CD=AB．
(1)求点D的坐标
（2）四边形OCDB的面积
(3)在y轴上是否存在一点P，使
＝
，若存在这样一点，求出点P的坐标，若不存在，试说明理由．
参考答案：
【答案】（1）D（4,2）；（2）7；（3）存在，P（0， 
）或（0， 
）
【解析】试题分析：（1）依题意知，将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，故C、D两点点y值为2. 所以可求点D的坐标；
（2）结合图形，根据梯形的面积公式求解；
（3）通过面积相等法，直接根据三角形的面积和四边形的面积可求解.
试题解析：（1）∵A（-1,0），B（3,0）
∴AB=4
∵CD=AB
∴CD=4
∵C（0,2），CD∥x轴
∴D（4,2）
（2）
=7
（3）存在，理由如下
设P（0，y）
∵
＝
∴
∴
∴
∴P（0， 
）或（0， 
）
-
科目： 来源： 题型：
查看答案和解析>>【题目】在0，2，﹣7，﹣5，3中，最小数的相反数是_____，绝对值最小的数是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数
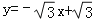的函数图象与x轴、y轴分别交于点A、B，以线段AB为直角边在第一象限内作Rt△ABC，且使∠ABC=30°；
（1）如果点P（m，
）在第二象限内，试用含m的代数式表示四边形AOPB的面积，并求当△APB与△ABC面积相等时m的值；（2）如果△QAB是等腰三角形并且点Q在坐标轴上，请求出点Q所有可能的坐标；
（3）是否存在实数a，b使一次函数
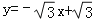和y=ax+b的图象关于直线y=x对称？若存在，求出
的值；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】市政府决定对市直机关500户家庭的用水情况作一次调查，市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量（单位：吨），并将调查结果制成了如图所示的条形统计图．
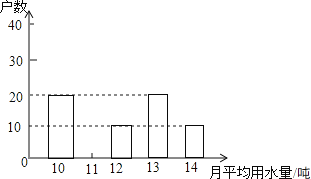
（1）请将条形统计图补充完整；
（2）求这100个样本数据的平均数，众数和中位数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（
，
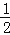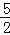）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．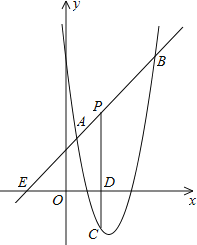
（1）求抛物线的解析式；
（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1是“东方之星”救援打捞现场图，小红据此构造出一个如图2所示的数学模型，已知：A、B、D三点在同一水平线上，CD⊥AD，∠A=30°，∠CBD=75°，AB=60m．
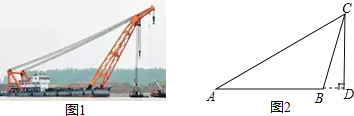
（1）求点B到AC的距离；
（2）求线段CD的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】鄂州市化工材料经销公司购进一种化工原料若干千克，价格为每千克30元．物价部门规定其销售单价不高于每千克60元，不低于每千克30元．经市场调查发现：日销售量y（千克）是销售单价x（元）的一次函数，且当x=60时，y=80；x=50时，y=100．在销售过程中，每天还要支付其他费用450元．
（1）求出y与x的函数关系式，并写出自变量x的取值范围．
（2）求该公司销售该原料日获利w（元）与销售单价x（元）之间的函数关系式．
（3）当销售单价为多少元时，该公司日获利最大？最大获利是多少元？
相关试题
