【题目】如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.
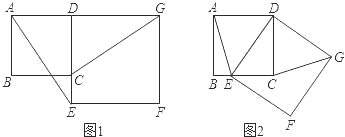
(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和GC.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
参考答案:
【答案】(1)AE⊥CE,证明见解析;(2)成立,证明见解析
【解析】
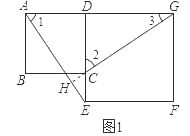
试题(1)观察图形,AE、CG的位置关系可能是垂直,下面着手证明.由于四边形ABCD、DEFG都是正方形,易证得△ADE≌△CDG,则∠1=∠2,由于∠2、∠3互余,所以∠1、∠3互余,由此可得AH⊥CG.
(2)题(1)的结论仍然成立,参照(1)题的解题方法,可证△ADE≌△CDG,得∠5=∠4,由于∠4、∠7互余,而∠5、∠6互余,那么∠6=∠7;由图知∠AEB=∠CEH=90°-∠6,即∠7+∠CEH=90°,由此得证.
试题解析:(1)AE⊥GC;
证明:延长GC交AE于点H,
在正方形ABCD与正方形DEFG中,
AD=DC,∠ADE=∠CDG=90°,
DE=DG,
∴△ADE≌△CDG,
∴∠1=∠2;
∵∠2+∠3=90°,
∴∠1+∠3=90°,
∴∠AHG=180°-(∠1+∠3)=180°-90°=90°,
∴AE⊥GC.
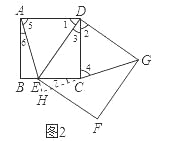
(2)成立;
证明:延长AE和GC相交于点H,
在正方形ABCD和正方形DEFG中,
AD=DC,DE=DG,∠ADC=∠DCB=∠B=∠BAD=∠EDG=90°,
∴∠1=∠2=90°-∠3;
∴△ADE≌△CDG,
∴∠5=∠4;
又∵∠5+∠6=90°,∠4+∠7=180°-∠DCE=180°-90°=90°,
∴∠6=∠7,
又∵∠6+∠AEB=90°,∠AEB=∠CEH,
∴∠CEH+∠7=90°,
∴∠EHC=90°,
∴AE⊥GC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
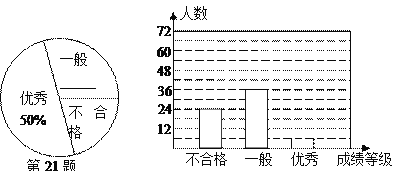
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ADC=90°,AD=8,CD=6,AB=26,BC=24.
(1)试说明:△ABC是直角三角形.
(2)请求图中阴影部分的面积.

-
科目: 来源: 题型:
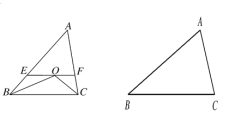
查看答案和解析>>【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过O做EF∥BC分别交AB、AC于E、F.
(1)求证:EF=BE+CF.
(2)在△ABC中,∠ABC的角平分线与∠ACB相邻的外角的平分线相交于点O,过O做EF∥BC分别交AB、AC于E、F,请你画出图形(不要求尺规作图),并直接写出EF、BE、CF之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,点A(0,1),点C(1,0),正方形AOCD的两条对角线的交点为B,延长BD至点G,使DG=BD,延长BC至点E,使CE=BC,以BG,BE为邻边作正方形BEFG.
(Ⅰ)如图①,求OD的长及
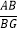 的值;
的值;(Ⅱ)如图②,正方形AOCD固定,将正方形BEFG绕点B逆时针旋转,得正方形BE′F′G′,记旋转角为α(0°<α<360°),连接AG′.
①在旋转过程中,当∠BAG′=90°时,求α的大小;
②在旋转过程中,求AF′的长取最大值时,点F′的坐标及此时α的大小(直接写出结果即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c.
(Ⅰ)若抛物线的顶点为A(﹣2,﹣4),抛物线经过点B(﹣4,0)
①求该抛物线的解析式;
②连接AB,把AB所在直线沿y轴向上平移,使它经过原点O,得到直线l,点P是直线l上一动点.
设以点A,B,O,P为顶点的四边形的面积为S,点P的横坐标为x,当4+6
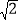 ≤S≤6+8
≤S≤6+8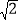 时,求x的取值范围;
时,求x的取值范围;(Ⅱ)若a>0,c>1,当x=c时,y=0,当0<x<c时,y>0,试比较ac与l的大小,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A可以用来解释
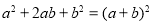 ,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.
,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.(1)图B可以解释的代数恒等式是 ;
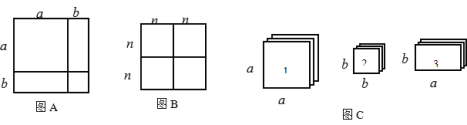
(2)现有足够多的正方形和矩形卡片,如图C:
①若要拼出一个面积为(3a+b)(a+2b)的矩形,则需要1号卡片 张,2号卡片 张,3号卡片 张;
②试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形,使该矩形的面积为6a2+7ab+2b2,并利用你画的图形面积对6a2+7ab+2b2进行因式分解.
相关试题

