【题目】已知抛物线y=ax2+bx+c.
(Ⅰ)若抛物线的顶点为A(﹣2,﹣4),抛物线经过点B(﹣4,0)
①求该抛物线的解析式;
②连接AB,把AB所在直线沿y轴向上平移,使它经过原点O,得到直线l,点P是直线l上一动点.
设以点A,B,O,P为顶点的四边形的面积为S,点P的横坐标为x,当4+6![]() ≤S≤6+8
≤S≤6+8![]() 时,求x的取值范围;
时,求x的取值范围;
(Ⅱ)若a>0,c>1,当x=c时,y=0,当0<x<c时,y>0,试比较ac与l的大小,并说明理由.
参考答案:
【答案】(Ⅰ)①y=x2+4x②当4+6![]() ≤S≤6+8
≤S≤6+8![]() 时,x的取值范围为是
时,x的取值范围为是![]() ≤x≤
≤x≤![]() 或
或![]() ≤x≤
≤x≤![]() (Ⅱ)ac≤1
(Ⅱ)ac≤1
【解析】
(I)①由抛物线的顶点为A(-2,-4),可设抛物线的解析式为y=a(x+2)2-4,代入点B的坐标即可求出a值,此问得解,②根据点A、B的坐标利用待定系数法可求出直线AB的解析式,进而可求出直线l的解析式,分点P在第二象限及点P在第四象限两种情况考虑:当点P在第二象限时,x<0,通过分割图形求面积法结合4+6![]() ≤S≤6+8
≤S≤6+8![]() ,即可求出x的取值范围,当点P在第四象限时,x>0,通过分割图形求面积法结合4+6≤S≤6+8
,即可求出x的取值范围,当点P在第四象限时,x>0,通过分割图形求面积法结合4+6≤S≤6+8![]() ,即可求出x的取值范围,综上即可得出结论,(2)由当x=c时y=0,可得出b=-ac-1,由当0<x<c时y>0,可得出抛物线的对称轴x=
,即可求出x的取值范围,综上即可得出结论,(2)由当x=c时y=0,可得出b=-ac-1,由当0<x<c时y>0,可得出抛物线的对称轴x=![]() ≥c,进而可得出b≤-2ac,结合b=-ac-1即可得出ac≤1.
≥c,进而可得出b≤-2ac,结合b=-ac-1即可得出ac≤1.
(I)①设抛物线的解析式为y=a(x+2)2﹣4,
∵抛物线经过点B(﹣4,0),
∴0=a(﹣4+2)2﹣4,
解得:a=1,
∴该抛物线的解析式为y=(x+2)2﹣4=x2+4x.
②设直线AB的解析式为y=kx+m(k≠0),
将A(﹣2,﹣4)、B(﹣4,0)代入y=kx+m,
得:![]() ,解得:
,解得:![]() ,
,
∴直线AB的解析式为y=﹣2x﹣8.
∵直线l与AB平行,且过原点,
∴直线l的解析式为y=﹣2x.
当点P在第二象限时,x<0,如图所示.
S△POB=![]() ×4×(﹣2x)=﹣4x,S△AOB=
×4×(﹣2x)=﹣4x,S△AOB=![]() ×4×4=8,
×4×4=8,
∴S=S△POB+S△AOB=﹣4x+8(x<0).
∵4+6![]() ≤S≤6+8
≤S≤6+8![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ≤x≤
≤x≤![]() ,
,
∴x的取值范围是![]() ≤x≤
≤x≤![]() .
.
当点P′在第四象限时,x>0,
过点A作AE⊥x轴,垂足为点E,过点P′作P′F⊥x轴,垂足为点F,则
S四边形AEOP′=S梯形AEFP′﹣S△OFP′=![]() (x+2)﹣
(x+2)﹣![]() x(2x)=4x+4.
x(2x)=4x+4.
∵S△ABE=![]() ×2×4=4,
×2×4=4,
∴S=S四边形AEOP′+S△ABE=4x+8(x>0).
∵4+6![]() ≤S≤6+8
≤S≤6+8![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ≤x≤
≤x≤![]() ,
,
∴x的取值范围为![]() ≤x≤
≤x≤![]() .
.
综上所述:当4+6![]() ≤S≤6+8
≤S≤6+8![]() 时,x的取值范围为是
时,x的取值范围为是![]() ≤x≤
≤x≤![]() 或
或![]() ≤x≤
≤x≤![]() .
.
(II)ac≤1,理由如下:
∵当x=c时,y=0,
∴ac2+bc+c=0,
∵c>1,
∴ac+b+1=0,b=﹣ac﹣1.
由x=c时,y=0,可知抛物线与x轴的一个交点为(c,0).
把x=0代入y=ax2+bx+c,得y=c,
∴抛物线与y轴的交点为(0,c).
∵a>0,
∴抛物线开口向上.
∵当0<x<c时,y>0,
∴抛物线的对称轴x=﹣![]() ≥c,
≥c,
∴b≤﹣2ac.
∵b=﹣ac﹣1,
∴﹣ac﹣1≤﹣2ac,
∴ac≤1.
-
科目: 来源: 题型:
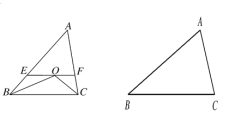
查看答案和解析>>【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过O做EF∥BC分别交AB、AC于E、F.
(1)求证:EF=BE+CF.
(2)在△ABC中,∠ABC的角平分线与∠ACB相邻的外角的平分线相交于点O,过O做EF∥BC分别交AB、AC于E、F,请你画出图形(不要求尺规作图),并直接写出EF、BE、CF之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.
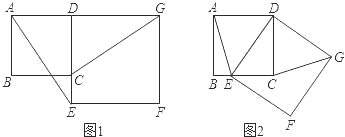
(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和GC.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,点A(0,1),点C(1,0),正方形AOCD的两条对角线的交点为B,延长BD至点G,使DG=BD,延长BC至点E,使CE=BC,以BG,BE为邻边作正方形BEFG.
(Ⅰ)如图①,求OD的长及
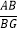 的值;
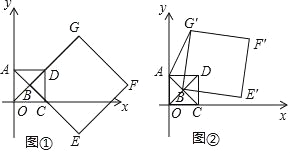
的值;(Ⅱ)如图②,正方形AOCD固定,将正方形BEFG绕点B逆时针旋转,得正方形BE′F′G′,记旋转角为α(0°<α<360°),连接AG′.
①在旋转过程中,当∠BAG′=90°时,求α的大小;
②在旋转过程中,求AF′的长取最大值时,点F′的坐标及此时α的大小(直接写出结果即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】 我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A可以用来解释
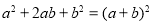 ,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.
,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.(1)图B可以解释的代数恒等式是 ;
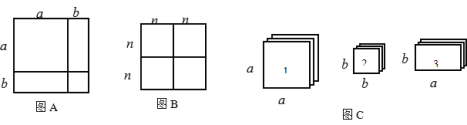
(2)现有足够多的正方形和矩形卡片,如图C:
①若要拼出一个面积为(3a+b)(a+2b)的矩形,则需要1号卡片 张,2号卡片 张,3号卡片 张;
②试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形,使该矩形的面积为6a2+7ab+2b2,并利用你画的图形面积对6a2+7ab+2b2进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinxcosy+cosxsiny.
据此判断下列等式成立的是 (写出所有正确的序号)
①cos(﹣60°)=﹣
 ;
;②sin75°=
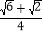 ;
;③sin2x=2sinxcosx;
④sin(x﹣y)=sinxcosy﹣cosxsiny.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
(2)现需要加装支架DE、EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为点F,求支架DE的长.

相关试题

